ГДЗ по Математике 6 Класс Часть 2 Номер 4.9 Виленкин, Жохов — Подробные Ответы

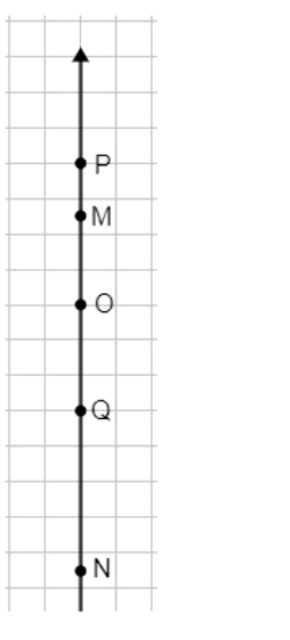
Проведите вертикальную прямую и отметьте
б на ней точку \(O\). Отметьте на этой прямой точки \(P, Q, M, N\), если известно, что:
а) точка \(P\) выше точки \(O\) на 4 клетки;
б) точка \(Q\) ниже точки \(O\) на 3 клетки;
в) точка \(M\) выше точки \(O\) на 2,5 клетки;
г) точка \(N\) ниже точки \(O\) на 7,5 клеток.

а) Точка \( P \) выше точки \( O \) на 4 клетки, значит \( P \) находится на 4 клетки выше \( O \).

б) Точка \( Q \) ниже точки \( O \) на 3 клетки, значит \( Q \) находится на 3 клетки ниже \( O \).

в) Точка \( M \) выше точки \( O \) на 2,5 клетки, значит \( M \) находится на 2,5 клетки выше \( O \).

г) Точка \( N \) ниже точки \( O \) на 7,5 клеток, значит \( N \) находится на 7,5 клеток ниже \( O \).

а) Здесь используется вертикальная «счётная линейка» клеток относительно опорной точки \(O\). Фраза «точка \(P\) выше точки \(O\) на 4 клетки» означает, что между \(P\) и \(O\) по вертикали ровно четыре одинаковых шага-клетки вверх. Если принять вертикальную ось вверх как положительное направление, то смещение точки \(P\) относительно \(O\) равно \(+4\) клетки, то есть \( \Delta y_{P/O}=+4 \). Это читается так: чтобы попасть из \(O\) в \(P\), нужно подняться на \(4\) клеток; обратный переход из \(P\) в \(O\) требует спуститься на \(4\) клеток, что эквивалентно смещению \( -4 \) клетки. Формулировка «\(P\) находится на 4 клетки выше \(O\)» полностью совпадает по смыслу с исходным описанием и корректно фиксирует направление и величину сдвига.

б) Аналогично, «точка \(Q\) ниже точки \(O\) на 3 клетки» указывает на вертикальное смещение вниз. Если вниз считать отрицательным направлением, то смещение точки \(Q\) относительно \(O\) равно \( -3 \) клетки, то есть \( \Delta y_{Q/O}=-3 \). Это означает: от \(O\) к \(Q\) нужно сделать \(3\) шага вниз, а от \(Q\) к \(O\) — \(3\) шага вверх, что можно записать как \( \Delta y_{O/Q}=+3 \). Поэтому вывод «\(Q\) находится на 3 клетки ниже \(O\)» точно отражает и направление (вниз), и величину (три клетки) вертикального сдвига.

в) В случае с точкой \(M\) используется дробное число клеток: «выше на \(2{,}5\) клетки» означает, что подъём состоит из двух полных клеток и ещё половины клетки. В координатной интерпретации это смещение \( \Delta y_{M/O}=+2{,}5 \) клетки. При необходимости эту величину можно записать дробью как \( \Delta y_{M/O}=+\frac{5}{2} \) клетки, что подчёркивает, что половина клетки — это ровно половина стандартного шага по вертикальной сетке. Следовательно, утверждение «\(M\) находится на 2{,}5 клетки выше \(O\)» корректно передаёт и величину, и направление смещения.

г) Для точки \(N\) указано «ниже точки \(O\) на \(7{,}5\) клеток», что читается как смещение вниз на семь полных клеток и ещё на половину клетки. В принятом знаковом соглашении это даёт \( \Delta y_{N/O}=-7{,}5 \) клетки, или в дробной записи \( \Delta y_{N/O}=-\frac{15}{2} \) клетки. Это означает: чтобы перейти из \(O\) к \(N\), нужно опуститься на \(7{,}5\) клетки, а вернуться обратно — подняться на \(7{,}5\) клетки. Формулировка «\(N\) находится на 7{,}5 клеток ниже \(O\)» полностью согласуется с описанным смещением.