ГДЗ по Математике 6 Класс Часть 2 Номер 4.78 Виленкин, Жохов — Подробные Ответы

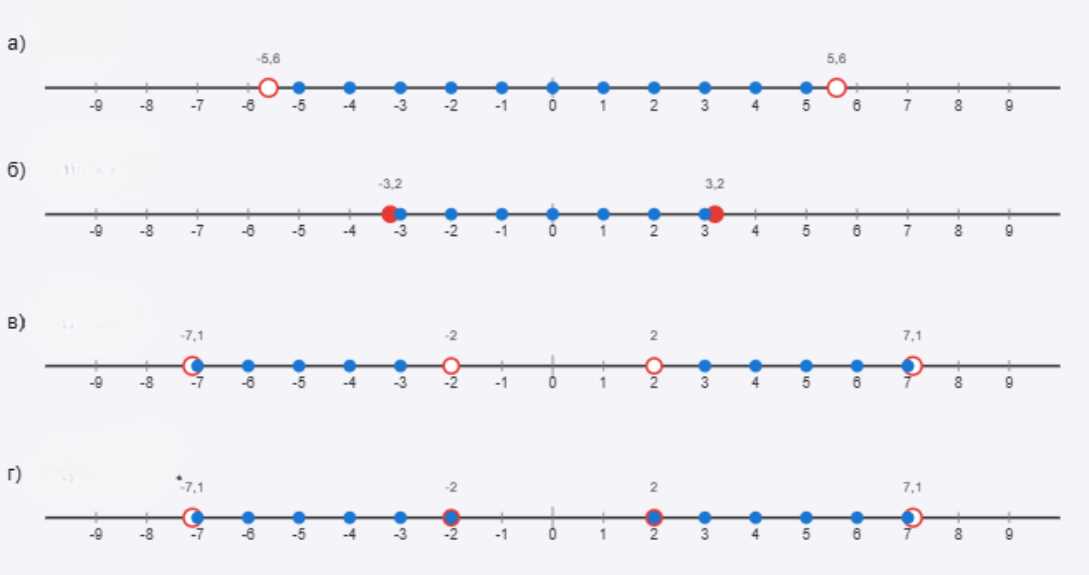
Отметьте на координатной прямой целые значения \(n\), при которых верно неравенство:  

а) \(|n| < 5,6\);  

б) \(|n| < 3,2\);  

в) \(2 < |n| < 7,1\);  

г) \(2 \leq n < 7,1\).

a) Условие: \(|n|<5{,}6\).
Так как \(n\) — целое, берём все целые с модулями меньше \(5{,}6\): \(n\in\{-5,-4,-3,-2,-1,0,1,2,3,4,5\}\).

б) Условие: \(|n|\le 3{,}2\).
Целые числа с модулями не больше \(3{,}2\): \(n\in\{-3,-2,-1,0,1,2,3\}\).

в) Условие: \(2<|n|<7{,}1\).
Исключаем \(|n|\le2\) и берём \(|n|<7{,}1\Rightarrow |n|\le7\): \(n\in\{-7,-6,-5,-4,-3,3,4,5,6,7\}\).

г) Условие: \(2\le|n|<7{,}1\).
Теперь допускаем \(|n|=2\) и снова \(|n|<7{,}1\Rightarrow |n|\le7\): \(n\in\{-7,-6,-5,-4,-3,-2,2,3,4,5,6,7\}\).

a) Рассматриваем неравенство \(|n|<5{,}6\). Модуль целого числа показывает расстояние от нуля на числовой прямой. Условие \(|n|<5{,}6\) означает, что точка \(n\) должна лежать строго внутри интервала \((-5{,}6;5{,}6)\). Так как \(n\) целое, берём все целые, попадающие внутрь этого интервала: крайние значения \(-6\) и \(6\) не подходят, поскольку их модуль равен \(6\), что не меньше \(5{,}6\). Подходят целые от \(-5\) до \(5\) включительно. Следовательно, \(n\in\{-5,-4,-3,-2,-1,0,1,2,3,4,5\}\).

б) Рассматриваем \(|n|\le 3{,}2\). Здесь граница включена, значит разрешены все целые числа, расстояние которых от нуля не превышает \(3{,}2\). Отметим, что ближайшие целые за пределами этой границы были бы \(-4\) и \(4\), но их модуль равен \(4\), что больше \(3{,}2\), поэтому они не подходят. На числовой прямой это все целые от \(-3\) до \(3\) включительно: \(-3,-2,-1,0,1,2,3\). Значит, \(n\in\{-3,-2,-1,0,1,2,3\}\).

в) Условие \(2<|n|<7{,}1\) задаёт «кольцевую» зону: отбрасываем все числа с \(|n|\le2\) и одновременно требуем, чтобы \(|n|\) было строго меньше \(7{,}1\). Так как \(n\) целое, верхняя строгая граница \(7{,}1\) эквивалентна требованию \(|n|\le7\). При этом из-за нижней строгой границы исключаем значения с модулями \(0,1,2\). Итак, допустимые модули: \(3,4,5,6,7\), что даёт симметричное множество отрицательных и положительных чисел, кроме нуля: \(-7,-6,-5,-4,-3,3,4,5,6,7\). Следовательно, \(n\in\{-7,-6,-5,-4,-3,3,4,5,6,7\}\).

г) В неравенстве \(2\le|n|<7{,}1\) нижняя граница уже нестрогая, поэтому числа с \(|n|=2\) допускаются. Верхняя граница остаётся строго меньше \(7{,}1\), что для целых снова означает \(|n|\le7\). Таким образом, допустимые модули: \(2,3,4,5,6,7\). Это даёт парные отрицательные и положительные значения, а ноль исключается, потому что \(|0|=0\) не удовлетворяет условию \(|n|\ge2\). Значит, \(n\in\{-7,-6,-5,-4,-3,-2,2,3,4,5,6,7\}\).