ГДЗ по Математике 6 Класс Часть 2 Номер 4.70 Виленкин, Жохов — Подробные Ответы

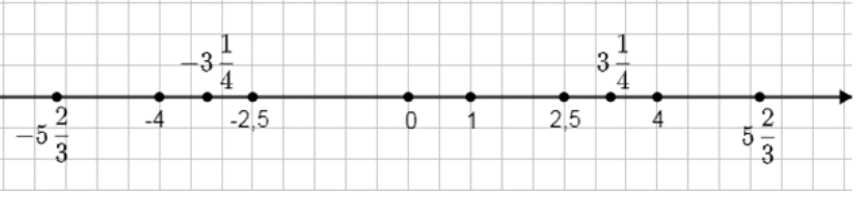
Отметьте на координатной прямой числа, модули которых равны 4, \(5 \frac{2}{3}\), \(3 \frac{1}{4}\), 2,5.

Для каждого уравнения с модулем используем определение: \(|m|=a\) означает два решения \(m=-a\) и \(m=a\).

1) \(|m|=4\). Решения: \(m=-4\) и \(m=4\).

2) \(|m|=2{,}5\). Решения: \(m=-2{,}5\) и \(m=2{,}5\).

3) \(|m|=5\frac{2}{3}\). Переведём в неправильную дробь: \(5\frac{2}{3}=\frac{17}{3}\). Решения: \(m=-\frac{17}{3}\) и \(m=\frac{17}{3}\).

4) \(|m|=3\frac{1}{4}\). Переведём в неправильную дробь: \(3\frac{1}{4}=\frac{13}{4}\). Решения: \(m=-\frac{13}{4}\) и \(m=\frac{13}{4}\).

Точки-решения отмечаются на числовой прямой симметрично относительно нуля в позициях \(-4,4\), \(-2{,}5,2{,}5\), \(-\frac{17}{3},\frac{17}{3}\), \(-\frac{13}{4},\frac{13}{4}\).

1) Определение модуля числа: модуль показывает расстояние от числа до нуля на числовой прямой и всегда неотрицателен. Поэтому равенство вида \(|m|=a\) с \(a>0\) означает, что точек на прямой две: одна на расстоянии \(a\) слева от нуля и другая на расстоянии \(a\) справа. Следовательно, \(|m|=4\) даёт два решения, потому что и \(m=-4\), и \(m=4\) находятся на расстоянии \(4\) от нуля: \(m=-4\) и \(m=4\). Эти точки симметричны относительно нуля, то есть середина отрезка между ними совпадает с \(0\), а их координаты равны по модулю и противоположны по знаку.

2) Для \(|m|=2{,}5\) рассуждения те же: расстояние \(2{,}5\) от нуля достигается в двух местах. Слева это \(m=-2{,}5\), справа это \(m=2{,}5\). Оба значения удовлетворяют определению модуля, так как \(|-2{,}5|=2{,}5\) и \(|2{,}5|=2{,}5\). На числовой прямой эти точки также образуют пару симметричных отметок вокруг нуля, причём каждая находится ровно на \(2{,}5\) единицы от него.

3) В записи \(|m|=5\frac{2}{3}\) удобнее перейти к неправильной дроби, чтобы избежать ошибок при вычислениях и точно указать координаты: \(5\frac{2}{3}=\frac{5\cdot3+2}{3}=\frac{17}{3}\). Тогда решение читается как две точки, отстоящие от нуля на \(\frac{17}{3}\): \(m=-\frac{17}{3}\) и \(m=\frac{17}{3}\). Проверка прямая: \(|-\frac{17}{3}|=\frac{17}{3}\) и \(|\frac{17}{3}|=\frac{17}{3}\). На числовой прямой это числа чуть больше \(5\) по модулю, так как \(\frac{17}{3}=5\frac{2}{3}\), и они отмечаются симметрично по разные стороны от нуля.

4) В уравнении \(|m|=3\frac{1}{4}\) также переводим смешанное число: \(3\frac{1}{4}=\frac{3\cdot4+1}{4}=\frac{13}{4}\). По определению модуля получаем два решения: \(m=-\frac{13}{4}\) и \(m=\frac{13}{4}\). Проверяем: \(|-\frac{13}{4}|=\frac{13}{4}\) и \(|\frac{13}{4}|=\frac{13}{4}\). Числа расположены на расстоянии \(\frac{13}{4}=3\frac{1}{4}\) от нуля влево и вправо соответственно, что полностью согласуется с разметкой на рисунке.

Итоговая совокупность решений по всем четырём пунктам образует по две точки на прямой в парах противоположных чисел: \(-4\) и \(4\); \(-2{,}5\) и \(2{,}5\); \(-\frac{17}{3}\) и \(\frac{17}{3}\); \(-\frac{13}{4}\) и \(\frac{13}{4}\). Все пары имеют равные модули и противоположные знаки, поэтому каждая пара симметрична относительно нуля, а расстояния от нуля строго равны указанным значениям модуля.