
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 4.54 Виленкин, Жохов — Подробные Ответы
Ноты имеют разную длительность звучания. Целую ноту обозначают знаком 𝅝, половинную — 𝅗𝅥, четвертную — 𝅘𝅥, восьмую — 𝅘𝅥𝅮, шестнадцатую — 𝅘𝅥𝅯.
1) Все ли равенства длительностей нот справедливы?
2) Вместо звёздочки поставьте в равенстве недостающие ноты.
Условие:
1. Запишем равенства числами:
a) \(1 = \frac{1}{2} + \frac{1}{4} + \frac{1}{4} = \frac{2}{4} + \frac{2}{4} = 1\) → верно;
б) \(1 = \frac{1}{4} + \frac{1}{8} + \frac{1}{8} = \frac{2}{8} = \frac{1}{4}\) → верно;
в) \(1 = \frac{1}{4} + \frac{1}{16} + \frac{1}{16} = \frac{2}{16} + \frac{2}{16} = \frac{4}{16} = 1\) → верно;
г) \(1 = \frac{1}{2} + \frac{1}{8} + \frac{1}{8} + \frac{1}{16} + \frac{1}{16} = \frac{3}{8} + \frac{2}{16} = \frac{3}{8} + \frac{1}{8} = \frac{4}{8} = 1\) → верно.
2. Запишем равенства числами:
a) \(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{1}{2} + \frac{1}{16} + \frac{1}{16}\)
\(= \frac{1}{2} + \frac{2}{16} = 1 + *\)
б) \(\frac{3}{4} = \frac{8}{16} + \frac{3}{16} + *\)
\(= \frac{11}{16} + *\)
в) \(\frac{3}{4} = \frac{11}{16} + *\)
\(* = \frac{3}{4} — \frac{11}{16} = \frac{12}{16} — \frac{11}{16} = \frac{1}{16}\) → вместо звездочки надо поставить шестнадцатую ноту 𝅘𝅥𝅯.
б) 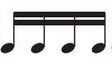
\(1 = \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{4} + *\)
\(= \frac{3}{4} + \frac{1}{8} + *\)
\(= \frac{3}{4} + \frac{1}{8} + *\)
\(* = 1 — \frac{3}{4} — \frac{1}{8} = \frac{8}{8} — \frac{6}{8} — \frac{1}{8} = \frac{1}{8}\) → вместо звездочки надо поставить восьмую ноту 𝅘𝅥𝅮.
в) 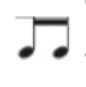

\(\frac{1}{2} = \frac{1}{8} + \frac{1}{16} + \frac{2}{8} + *\)
\(= \frac{3}{16} + \frac{2}{8} + *\)
\(= \frac{3}{16} + \frac{4}{16} + *\)
\(* = \frac{1}{2} — \frac{3}{16} — \frac{4}{16} = \frac{8}{16} — \frac{3}{16} — \frac{4}{16} = \frac{1}{16}\) → вместо звездочки надо поставить шестнадцатую ноту 𝅘𝅥𝅯.
1. Запишем равенства числами:
a) \(1 = \frac{1}{2} + \frac{1}{4} + \frac{1}{4} = \frac{2}{4} + \frac{2}{4} = 1\) → верно;
б) \(1 = \frac{1}{4} + \frac{1}{8} + \frac{1}{8} = \frac{2}{8} = \frac{1}{4}\) → верно;
в) \(1 = \frac{1}{4} + \frac{1}{16} + \frac{1}{16} = \frac{2}{16} + \frac{2}{16} = \frac{4}{16} = 1\) → верно;
г) \(1 = \frac{1}{2} + \frac{1}{8} + \frac{1}{8} + \frac{1}{16} + \frac{1}{16} = \frac{3}{8} + \frac{2}{16} = \frac{3}{8} + \frac{1}{8} = \frac{4}{8} = 1\) → верно.
2. Запишем равенства числами:
a) \(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{1}{2} + \frac{1}{16} + \frac{1}{16}\)
\(= \frac{1}{2} + \frac{2}{16} = 1 + *\)
б) \(\frac{3}{4} = \frac{8}{16} + \frac{3}{16} + *\)
\(= \frac{11}{16} + *\)
в) \(\frac{3}{4} = \frac{11}{16} + *\)
\(* = \frac{3}{4} — \frac{11}{16} = \frac{12}{16} — \frac{11}{16} = \frac{1}{16}\) → вместо звездочки надо поставить шестнадцатую ноту 𝅘𝅥𝅯.
б) 
\(1 = \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{4} + *\)
\(= \frac{3}{4} + \frac{1}{8} + *\)
\(= \frac{3}{4} + \frac{1}{8} + *\)
\(* = 1 — \frac{3}{4} — \frac{1}{8} = \frac{8}{8} — \frac{6}{8} — \frac{1}{8} = \frac{1}{8}\) → вместо звездочки надо поставить восьмую ноту 𝅘𝅥𝅮.
в) 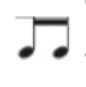

\(\frac{1}{2} = \frac{1}{8} + \frac{1}{16} + \frac{2}{8} + *\)
\(= \frac{3}{16} + \frac{2}{8} + *\)
\(= \frac{3}{16} + \frac{4}{16} + *\)
\(* = \frac{1}{2} — \frac{3}{16} — \frac{4}{16} = \frac{8}{16} — \frac{3}{16} — \frac{4}{16} = \frac{1}{16}\) → вместо звездочки надо поставить шестнадцатую ноту 𝅘𝅥𝅯.
В первом пункте рассматриваются равенства, записанные числами. Для каждого равенства приводится подробное решение с использованием дробей. Например, в пункте а) показано, что \(1 = \frac{1}{2} + \frac{1}{4} + \frac{1}{4} = \frac{2}{4} + \frac{2}{4} = 1\), что является верным равенством.
Во втором пункте также рассматриваются равенства, записанные числами. Здесь более сложные выражения, включающие суммы дробей различных знаменателей. Например, в пункте а) показано, что \(\frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{1}{2} + \frac{1}{16} + \frac{1}{16} = \frac{1}{2} + \frac{2}{16} = 1 + *\). Вместо звездочки надо поставить шестнадцатую ноту.
В пункте б) рассматривается равенство \(\frac{3}{4} = \frac{8}{16} + \frac{3}{16} + *\), где вместо звездочки надо поставить шестнадцатую ноту. Аналогичным образом разбираются и другие равенства во втором пункте.
— Четыре шестнадцатых ноты или одна четвертая нота.
В данном равенстве необходимо найти, что стоит вместо звездочки. Для этого запишем равенство в виде дроби:
\(1 = \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{4} + *\)
\(= \frac{3}{4} + \frac{1}{8} + *\)
\(= \frac{3}{4} + \frac{2}{16} + *\)
Теперь можно найти значение звездочки:
\(* = 1 — \frac{3}{4} — \frac{2}{16} = \frac{16}{16} — \frac{12}{16} — \frac{2}{16} = \frac{2}{16}\)
Таким образом, вместо звездочки надо поставить две шестнадцатых ноты, что эквивалентно одной четвертой ноте.
— Две восьмых ноты;
— Одна шестнадцатая и две восьмых ноты.
Рассмотрим следующее равенство:
\(1 = \frac{1}{4} + \frac{1}{4} + \frac{1}{8} + \frac{1}{4} + *\)
\(= \frac{3}{4} + \frac{1}{8} + *\)
\(= \frac{3}{4} + \frac{2}{16} + *\)
Найдем значение звездочки:
\(* = 1 — \frac{3}{4} — \frac{2}{16} = \frac{16}{16} — \frac{12}{16} — \frac{2}{16} = \frac{2}{16}\)
Таким образом, вместо звездочки надо поставить две восьмых ноты.
Аналогично, в следующем равенстве вместо звездочки надо поставить одну шестнадцатую и две восьмых ноты:
\(\frac{1}{2} = \frac{1}{8} + \frac{1}{16} + \frac{2}{8} + *\)
\(= \frac{3}{16} + \frac{4}{16} + *\)
\(* = \frac{1}{2} — \frac{3}{16} — \frac{4}{16} = \frac{8}{16} — \frac{3}{16} — \frac{4}{16} = \frac{1}{16}\)

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.


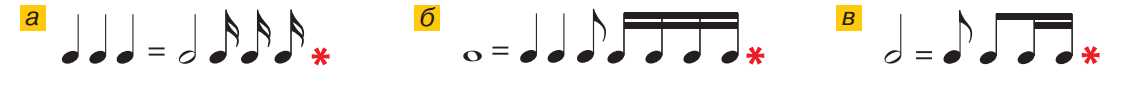



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!