
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 4.43 Виленкин, Жохов — Подробные Ответы
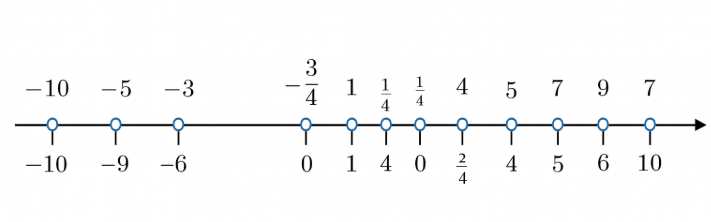
Заполните таблицу. Отметьте эти числа на координатной прямой.
1) Строим вторую строку по правилу противоположных чисел: для каждого \(x\) берём \(-x\). Получаем пары: \(3\rightarrow -3\), \(-4\rightarrow 4\), \(9\rightarrow -9\), \(-7{,}5\rightarrow 7{,}5\), \(-5\rightarrow 5\), \(-1\frac{1}{2}\rightarrow 1\frac{1}{2}\), \(2\frac{3}{4}\rightarrow -2\frac{3}{4}\), \(6\rightarrow -6\), \(0\rightarrow 0\), \(\frac{1}{4}\rightarrow -\frac{1}{4}\), \(1\rightarrow -1\), \(\frac{3}{4}\rightarrow -\frac{3}{4}\), \(-10\rightarrow 10\).
2) Итоговая таблица соответствует правилу \(x \mapsto -x\) и совпадает с разметкой на прямой: отрицательные и положительные значения симметричны относительно \(0\).
| x | 3 | -4 | 9 | -7,5 | -5 | -1\(\frac{1}{2}\) |
| -x | -3 | 4 | -9 | 7,5 | 5 | 1\(\frac{1}{2}\) |
| x | 2\(\frac{3}{4}\) | 6 | 0 | \(\frac{1}{4}\) | 1 | \(\frac{3}{4}\) | -10 |
| -x | -2\(\frac{3}{4}\) | -6 | 0 | -\(\frac{1}{4}\) | -1 | -\(\frac{3}{4}\) | 10 |
1) Правило построения второй строки основано на операции взятия противоположного числа: каждому значению \(x\) сопоставляем число \(-x\). Это означает, что числа одинаковы по модулю и имеют противоположные знаки, а \(0\) остаётся самим собой, так как \( -0 = 0\). Последовательно применяя правило к каждому элементу исходного набора, получаем пары: \(3 \rightarrow -3\), \(-4 \rightarrow 4\), \(9 \rightarrow -9\), \(-7{,}5 \rightarrow 7{,}5\), \(-5 \rightarrow 5\), \(-1\frac{1}{2} \rightarrow 1\frac{1}{2}\), \(2\frac{3}{4} \rightarrow -2\frac{3}{4}\), \(6 \rightarrow -6\), \(0 \rightarrow 0\), \(\frac{1}{4} \rightarrow -\frac{1}{4}\), \(1 \rightarrow -1\), \(\frac{3}{4} \rightarrow -\frac{3}{4}\), \(-10 \rightarrow 10\). Здесь важно понимать, что смешанные дроби читаются как сумма целой и дробной частей: например, \(-1\frac{1}{2} = -(1+\frac{1}{2})\) и при смене знака даёт \(1+\frac{1}{2}\), а \(2\frac{3}{4} = 2+\frac{3}{4}\) превращается в \(-(2+\frac{3}{4})\).
2) Геометрически преобразование \(x \mapsto -x\) есть осевая симметрия относительно нуля на координатной прямой: точка с координатой \(x\) переходит в точку на таком же расстоянии от нуля, но по другую сторону, то есть на координату \(-x\). Поэтому пары \(x\) и \(-x\) лежат симметрично: \((3,-3)\), \((-4,4)\), \((9,-9)\), \((-7{,}5,7{,}5)\), \((-5,5)\), \((-1\frac{1}{2},1\frac{1}{2})\), \((2\frac{3}{4},-2\frac{3}{4})\), \((6,-6)\), \((0,0)\), \((\frac{1}{4},-\frac{1}{4})\), \((1,-1)\), \((\frac{3}{4},-\frac{3}{4})\), \((-10,10)\). Ноль выступает центром симметрии и единственным числом, равным своему противоположному: \(0 = -0\). Дробные значения сохраняют модуль: \(\left|\frac{1}{4}\right| = \left|-\frac{1}{4}\right|\), так же как и смешанные дроби: \(\left|2\frac{3}{4}\right| = \left|-2\frac{3}{4}\right|\).
3) Итоговая таблица фиксирует исходные значения в первой строке и их противоположные во второй. Порядок элементов сохраняется, чтобы наглядно увидеть соответствие каждой пары \(x \leftrightarrow -x\). Числа с запятой, такие как \(-7{,}5\), трактуются как десятичные дроби и меняют только знак, а их абсолютная величина остаётся прежней. Такой формат позволяет сразу проверить корректность: для каждого столбца сумма чисел из двух строк равна нулю, то есть \(x + (-x) = 0\).
| x | 3 | -4 | 9 | -7,5 | -5 | -1\(\frac{1}{2}\) |
| -x | -3 | 4 | -9 | 7,5 | 5 | 1\(\frac{1}{2}\) |
| x | 2\(\frac{3}{4}\) | 6 | 0 | \(\frac{1}{4}\) | 1 | \(\frac{3}{4}\) | -10 |
| -x | -2\(\frac{3}{4}\) | -6 | 0 | -\(\frac{1}{4}\) | -1 | -\(\frac{3}{4}\) | 10 |

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!