ГДЗ по Математике 6 Класс Часть 2 Номер 4.34 Виленкин, Жохов — Подробные Ответы

Начертите шкалу температур от -40 до 40 °С, приняв отрезок длиной 1 см за 10 °С. Отметьте на этой шкале:
а) нормальную температуру кошки (39 °С);
б) температуру замерзания ртути (-39 °С);
в) температуру замерзания 50%-го раствора уксусной кислоты (-22 °С);
г) температуру кипения эфира (35 °С);
д) температуру кипения хлора (-34 °С).

1) Построим вертикальную шкалу от \(-40^\circ\text{C}\) до \(40^\circ\text{C}\), выбрав масштаб: \(1\,\text{см} \rightarrow 10^\circ\text{C}\). Нулевую отметку поставим по центру, через каждые \(10^\circ\text{C}\) — деления.

2) По заданным температурам ставим точки на соответствующих делениях и подписываем:
— а) \(39^\circ\text{C}\) — на делении чуть ниже \(40^\circ\text{C}\) (на \(1^\circ\text{C}\) ниже).
— б) \(-39^\circ\text{C}\) — на делении чуть выше \(-40^\circ\text{C}\) (на \(1^\circ\text{C}\) выше).
— в) \(-22^\circ\text{C}\) — между \(-20^\circ\text{C}\) и \(-30^\circ\text{C}\), ближе к \(-20^\circ\text{C}\) на \(2^\circ\text{C}\).
— г) \(35^\circ\text{C}\) — посередине между \(30^\circ\text{C}\) и \(40^\circ\text{C}\), но на \(5^\circ\text{C}\) выше \(30^\circ\text{C}\).
— д) \(-34^\circ\text{C}\) — между \(-30^\circ\text{C}\) и \(-40^\circ\text{C}\), на \(4^\circ\text{C}\) ниже \(-30^\circ\text{C}\).

Ответ: точки на шкале в положениях \(39\), \(-39\), \(-22\), \(35\), \(-34\) градусов Цельсия соответственно.

1) Задаем масштаб: отрезок длиной \(1\,\text{см}\) соответствует \(10^\circ\text{C}\). Это значит, что для каждого изменения температуры на \(1^\circ\text{C}\) нужно откладывать \(\frac{1}{10}\,\text{см}=1\,\text{мм}\). Построим вертикальную ось, отмечая крупные деления через \(10^\circ\text{C}\): \(-40,-30,-20,-10,0,10,20,30,40\). Нуль располагаем посередине отрезка, чтобы вверх были положительные температуры, а вниз — отрицательные. Между крупными делениями на каждом сантиметре делаем мелкие риски через \(1\,\text{мм}\), каждая из которых равна \(1^\circ\text{C}\). Это обеспечит точность постановки точек на произвольных целых значениях температуры.

2) Отмечаем заданные температуры по масштабу. Для \(39^\circ\text{C}\): от нуля поднимаемся на \(30^\circ\text{C}\) (три сантиметра), затем еще на \(9^\circ\text{C}\) (девять миллиметров). Точка будет на одном миллиметре ниже отметки \(40^\circ\text{C}\); подпись \(39^\circ\text{C}\). Для \(35^\circ\text{C}\): от нуля вверх на \(30^\circ\text{C}\) и еще на \(5^\circ\text{C}\) (пять миллиметров); это ровно посередине между \(30^\circ\text{C}\) и \(40^\circ\text{C}\) плюс \(5^\circ\text{C}\) от нижней границы десятка. Обе точки находятся в верхней (положительной) части шкалы, и их порядок сверху вниз: \(39^\circ\text{C}\) выше, \(35^\circ\text{C}\) ниже, потому что \(39>35\).

3) Для отрицательных значений двигаемся вниз от нуля. Температура \(-22^\circ\text{C}\): опускаемся на \(20^\circ\text{C}\) (два сантиметра) и еще на \(2^\circ\text{C}\) (два миллиметра) ниже отметки \(-20^\circ\text{C}\); точка ближе к \(-20^\circ\text{C}\), чем к \(-30^\circ\text{C}\). Температура \(-34^\circ\text{C}\): от нуля вниз на \(30^\circ\text{C}\) и еще на \(4^\circ\text{C}\) (четыре миллиметра); точка расположена между \(-30^\circ\text{C}\) и \(-40^\circ\text{C}\), на \(6\,\text{мм}\) выше \(-40^\circ\text{C}\). Температура \(-39^\circ\text{C}\): от нуля вниз на \(30^\circ\text{C}\) и еще на \(9^\circ\text{C}\) (девять миллиметров); это всего в \(1\,\text{мм}\) выше отметки \(-40^\circ\text{C}\). Их порядок сверху вниз в отрицательной зоне: \(-22^\circ\text{C}\), \(-34^\circ\text{C}\), \(-39^\circ\text{C}\).

4) Проверка соответствия масштабу: каждое целое изменение температуры на \(10^\circ\text{C}\) совпадает с \(1\,\text{см}\). Для любых двух отмеченных значений разность по шкале равна их модулю, умноженному на \(\frac{1}{10}\,\text{см}/^\circ\text{C}\). Например, расстояние между \(39^\circ\text{C}\) и \(35^\circ\text{C}\) равно \(|39-35|=4^\circ\text{C}\), что по линейке дает \(4\,\text{мм}\). Между \(-39^\circ\text{C}\) и \(-34^\circ\text{C}\) расстояние \(|-39-(-34)|=5^\circ\text{C}=5\,\text{мм}\). Между \(0^\circ\text{C}\) и \(-22^\circ\text{C}\) расстояние \(|0-(-22)|=22^\circ\text{C}=2\,\text{см}\,2\,\text{мм}\). Эти проверки подтверждают корректное размещение точек.

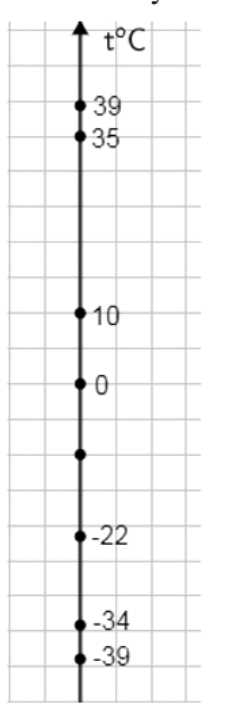
5) Итоговое размещение на построенной шкале от \(-40^\circ\text{C}\) до \(40^\circ\text{C}\) при масштабе \(1\,\text{см}\rightarrow10^\circ\text{C}\): вверху положительной части — точки \(39^\circ\text{C}\) и \(35^\circ\text{C}\) на соответствующих отметках; ниже нуля — точки \(-22^\circ\text{C}\), \(-34^\circ\text{C}\), \(-39^\circ\text{C}\) на указанных расстояниях от ближайших десятков. Расстановка соответствует изображению: \(39,35,10,0,-22,-34,-39\) по вертикали с подписями в градусах Цельсия.