
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 4.3 Виленкин, Жохов — Подробные Ответы
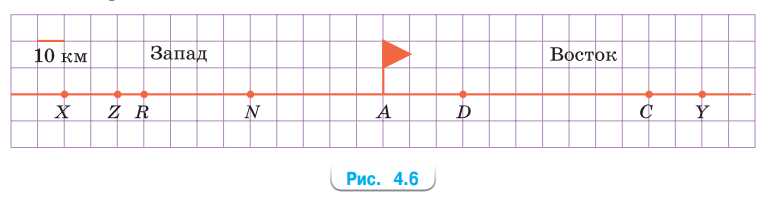
Опишите положение пунктов X, Z, R, N, D, C и Y (см. рис. 4.6) по отношению к пункту А.
1) Пункт \(X\) расположен на \(120\) км западнее пункта \(A\), значит координата \(X = A — 120\).
2) Пункт \(Z\) расположен на \(100\) км западнее пункта \(A\), значит координата \(Z = A — 100\).
3) Пункт \(R\) расположен на \(90\) км западнее пункта \(A\), значит координата \(R = A — 90\).
4) Пункт \(N\) расположен на \(50\) км западнее пункта \(A\), значит координата \(N = A — 50\).
5) Пункт \(D\) расположен на \(30\) км восточнее пункта \(A\), значит координата \(D = A + 30\).
6) Пункт \(C\) расположен на \(100\) км восточнее пункта \(A\), значит координата \(C = A + 100\).
7) Пункт \(Y\) расположен на \(120\) км восточнее пункта \(A\), значит координата \(Y = A + 120\).
1) Пункт \(X\) расположен на 120 км западнее пункта \(A\). Это значит, что если взять точку \(A\) за начало отсчёта с координатой \(A\), то точка \(X\) будет смещена влево (на запад) на 120 км. В координатной прямой, где движение на запад соответствует уменьшению значения, координата \(X\) будет равна \(A — 120\). Таким образом, положение \(X\) относительно \(A\) можно записать как \(X = A — 120\).
2) Пункт \(Z\) расположен на 100 км западнее пункта \(A\). Аналогично первому случаю, движение на запад уменьшает координату, поэтому для \(Z\) имеем \(Z = A — 100\). Это значит, что \(Z\) находится ближе к \(A\), чем \(X\), так как расстояние меньше. Координаты показывают, что \(Z\) располагается правее \(X\), но всё ещё западнее \(A\).
3) Пункт \(R\) расположен на 90 км западнее пункта \(A\). Следуя той же логике, координата \(R\) будет \(R = A — 90\). Это положение ещё ближе к \(A\), чем \(Z\) и \(X\), так как 90 км меньше 100 и 120 км. Таким образом, на координатной оси точки \(X, Z, R\) идут в порядке убывания расстояния от \(A\) на запад: \(X, Z, R\).
4) Пункт \(N\) расположен на 50 км западнее пункта \(A\). Здесь расстояние ещё меньше, значит \(N\) находится ближе к \(A\), чем все предыдущие пункты на запад. Координата \(N = A — 50\) показывает, что \(N\) находится между \(A\) и \(R\) на западной стороне.
5) Пункт \(D\) расположен на 30 км восточнее пункта \(A\). В отличие от предыдущих, движение на восток увеличивает координату. Значит, \(D\) находится справа от \(A\) на 30 км, и его координата будет \(D = A + 30\). Это первый пункт, расположенный восточнее \(A\).
6) Пункт \(C\) расположен на 100 км восточнее пункта \(A\). Координата \(C = A + 100\) показывает, что он расположен значительно дальше на восток, чем \(D\). Расстояние от \(A\) до \(C\) больше, чем до \(D\), следовательно, \(C\) находится правее \(D\).
7) Пункт \(Y\) расположен на 120 км восточнее пункта \(A\). Это самый восточный пункт из всех перечисленных. Его координата равна \(Y = A + 120\). Таким образом, на восточной стороне точки располагаются в порядке увеличения расстояния от \(A\) \(D, C, Y\).
Итог: все пункты можно представить на координатной оси с точкой \(A\) в центре, где западные пункты имеют координаты \(A — d\), а восточные — \(A + d\), где \(d\) — расстояние от \(A\). Это позволяет легко сравнивать положения и расстояния между пунктами.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!