ГДЗ по Математике 6 Класс Часть 2 Номер 4.290 Виленкин, Жохов — Подробные Ответы

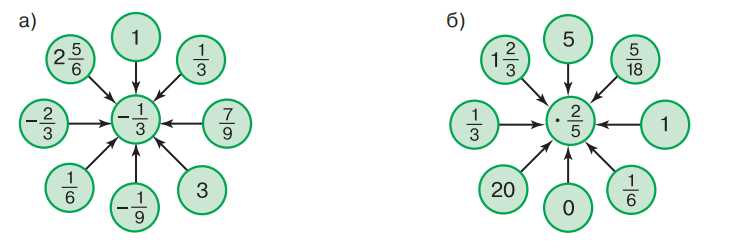
Вычислите:

а)
\(1 — \frac{1}{3} = \frac{2}{3}\);

\(\frac{1}{3} — \frac{1}{3} = 0\);

\(\frac{7}{9} — \frac{1}{3} = \frac{7}{9} — \frac{3}{9} = \frac{4}{9}\);

\(3 — \frac{1}{3} = 2 \frac{2}{3}\);

\(-\frac{1}{9} — \frac{1}{3} = -\frac{1}{9} — \frac{3}{9} = -\left(\frac{1}{9} + \frac{3}{9}\right) = -\frac{4}{9}\);

\(\frac{1}{6} — \frac{1}{3} = \frac{1}{6} — \frac{2}{6} = -\left(\frac{2}{6} — \frac{1}{6}\right) = -\frac{1}{6}\);

\(-\frac{2}{3} — \frac{1}{3} = -\left(\frac{2}{3} + \frac{1}{3}\right) = -1\);

\(2 \frac{5}{6} — \frac{1}{3} = 2 \frac{5}{6} — \frac{2}{6} = 2 \frac{3}{6} = 2 \frac{1}{2} = 2,5\).

б)
\(5 \cdot \frac{2}{5} = 2\);

\(\frac{5}{18} \cdot \frac{2}{5} = \frac{1}{9}\);

\(1 \cdot \frac{2}{5} = \frac{2}{5}\);

\(\frac{1}{6} \cdot \frac{2}{5} = \frac{2}{30} = \frac{1}{15}\);

\(0 \cdot \frac{2}{5} = 0\);

\(20 \cdot \frac{2}{5} = \frac{20 \cdot 2}{5} = \frac{40}{5} = 8\);

\(\frac{1}{3} \cdot \frac{2}{5} = \frac{2}{15}\);

\(\frac{2}{3} \cdot \frac{2}{5} = \frac{4}{15}\).

а)
Рассмотрим выражение \(1 — \frac{1}{3}\). Чтобы вычесть дробь из целого числа, представим 1 как дробь с тем же знаменателем: \(1 = \frac{3}{3}\). Тогда вычитание будет \( \frac{3}{3} — \frac{1}{3} = \frac{2}{3}\). Это объясняет, почему результат равен \( \frac{2}{3} \).

Далее, при вычислении \(\frac{1}{3} — \frac{1}{3}\), знаменатели уже одинаковые, поэтому просто вычитаем числители: \(1 — 1 = 0\). Значит, результат равен 0.

Для примера \(\frac{7}{9} — \frac{1}{3}\) сначала приводим вторую дробь к общему знаменателю с первой. Знаменатель 3 умножаем на 3, чтобы получить 9, значит \(\frac{1}{3} = \frac{3}{9}\). Теперь вычитаем: \(\frac{7}{9} — \frac{3}{9} = \frac{4}{9}\).

Рассмотрим \(3 — \frac{1}{3}\). Здесь 3 можно представить как \( \frac{9}{3}\). Тогда вычитание: \(\frac{9}{3} — \frac{1}{3} = \frac{8}{3}\), что в смешанной дроби равно \(2 \frac{2}{3}\).

Для выражения \(-\frac{1}{9} — \frac{1}{3}\) сначала приводим \(\frac{1}{3}\) к знаменателю 9: \(\frac{1}{3} = \frac{3}{9}\). Тогда сумма будет \(-\frac{1}{9} — \frac{3}{9} = -\left(\frac{1}{9} + \frac{3}{9}\right) = -\frac{4}{9}\).

Вычисление \(\frac{1}{6} — \frac{1}{3}\) требует приведения к общему знаменателю 6, так как \( \frac{1}{3} = \frac{2}{6}\). Тогда получаем: \(\frac{1}{6} — \frac{2}{6} = -\left(\frac{2}{6} — \frac{1}{6}\right) = -\frac{1}{6}\).

Вычитание \(-\frac{2}{3} — \frac{1}{3}\) складывает отрицательные дроби: \(-\left(\frac{2}{3} + \frac{1}{3}\right) = -1\).

Последнее выражение \(2 \frac{5}{6} — \frac{1}{3}\) сначала переводим смешанную дробь в неправильную: \(2 \frac{5}{6} = \frac{17}{6}\). Приводим \(\frac{1}{3}\) к знаменателю 6: \(\frac{1}{3} = \frac{2}{6}\). Вычитаем: \(\frac{17}{6} — \frac{2}{6} = \frac{15}{6} = 2 \frac{3}{6} = 2 \frac{1}{2} = 2,5\).

б)
В выражении \(5 \cdot \frac{2}{5}\) происходит умножение целого числа на дробь. Чтобы умножить, умножаем числитель на 5 и делим на знаменатель 5, то есть \(5 \cdot \frac{2}{5} = \frac{5 \cdot 2}{5} = 2\).

При умножении \(\frac{5}{18} \cdot \frac{2}{5}\) сокращаем 5 в числителе и знаменателе: \(\frac{5}{18} \cdot \frac{2}{5} = \frac{2}{18} = \frac{1}{9}\).

Умножение \(1 \cdot \frac{2}{5}\) просто равно самой дроби, так как 1 — это нейтральный элемент умножения: \(1 \cdot \frac{2}{5} = \frac{2}{5}\).

Вычислим \(\frac{1}{6} \cdot \frac{2}{5}\). Перемножаем числители и знаменатели: \(\frac{1 \cdot 2}{6 \cdot 5} = \frac{2}{30} = \frac{1}{15}\).

Умножение \(0 \cdot \frac{2}{5}\) всегда равно нулю, так как любое число, умноженное на 0, даёт 0.

Для \(20 \cdot \frac{2}{5}\) умножаем 20 на числитель 2 и делим на знаменатель 5: \(\frac{20 \cdot 2}{5} = \frac{40}{5} = 8\).

При умножении \(\frac{1}{3} \cdot \frac{2}{5}\) перемножаем числители и знаменатели: \(\frac{1 \cdot 2}{3 \cdot 5} = \frac{2}{15}\).

Наконец, \(\frac{2}{3} \cdot \frac{2}{5} = \frac{2 \cdot 2}{3 \cdot 5} = \frac{4}{15}\).