
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 4.251 Виленкин, Жохов — Подробные Ответы
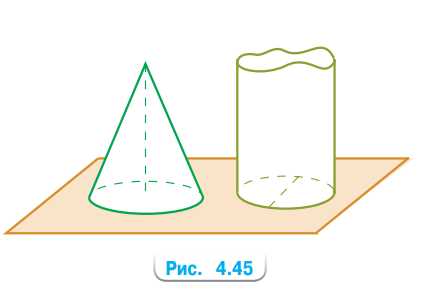
У конуса и цилиндра равные основания и объёмы. Найдите высоту цилиндра, если высота конуса 36 см (рис. 4.45).
1. Объем конуса \( V_{\text{конуса}} = \frac{1}{3} S_{\text{осн.}} h \); объем цилиндра \( V_{\text{цилиндра}} = S_{\text{осн.}} h \).
2. Известно, что \( V_{\text{конуса}} = V_{\text{цилиндра}} \), \( S_{\text{осн. кон.}} = S_{\text{осн. цил.}} \), \( h_{\text{кон.}} = 36 \text{ см} \).
3. Тогда:
\(\frac{1}{3} S_{\text{осн. кон.}} h_{\text{кон.}} = S_{\text{осн. цил.}} h_{\text{цил.}}\)
\(\frac{1}{3} h_{\text{кон.}} = h_{\text{цил.}}\)
\(\frac{1}{3} \cdot 36 = h_{\text{цил.}}\)
4. Получаем:
\(h_{\text{цил.}} = 12 \text{ см}\) — высота цилиндра.
Ответ: 12 см
1. Рассмотрим формулы для объёмов конуса и цилиндра. Объём конуса вычисляется по формуле \( V_{\text{конуса}} = \frac{1}{3} S_{\text{осн.}} h \), где \( S_{\text{осн.}} \) — площадь основания, а \( h \) — высота конуса. Для цилиндра объём равен \( V_{\text{цилиндра}} = S_{\text{осн.}} h \), где \( S_{\text{осн.}} \) — площадь основания цилиндра, а \( h \) — высота цилиндра. Таким образом, объём конуса составляет треть объёма цилиндра при одинаковой площади основания и высоте.
2. В условии задачи сказано, что объёмы конуса и цилиндра равны: \( V_{\text{конуса}} = V_{\text{цилиндра}} \). Кроме того, площади оснований у конуса и цилиндра тоже равны: \( S_{\text{осн. кон.}} = S_{\text{осн. цил.}} \). Известна высота конуса \( h_{\text{кон.}} = 36 \) см. Поскольку площади оснований равны, можно подставить их в уравнение равенства объёмов и получить:
\(\frac{1}{3} S_{\text{осн. кон.}} h_{\text{кон.}} = S_{\text{осн. цил.}} h_{\text{цил.}}\), то есть
\(\frac{1}{3} S_{\text{осн.}} h_{\text{кон.}} = S_{\text{осн.}} h_{\text{цил.}}\).
3. Упрощая уравнение, сокращаем площадь основания, так как она одинаковая:
\(\frac{1}{3} h_{\text{кон.}} = h_{\text{цил.}}\). Подставляем значение высоты конуса:
\(\frac{1}{3} \cdot 36 = h_{\text{цил.}}\). Вычисляем:
\(h_{\text{цил.}} = 12 \text{ см}\). Это и есть высота цилиндра, при которой объёмы двух тел равны при равных площадях оснований.
Ответ: 12 см

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!