ГДЗ по Математике 6 Класс Часть 2 Номер 4.16 Виленкин, Жохов — Подробные Ответы

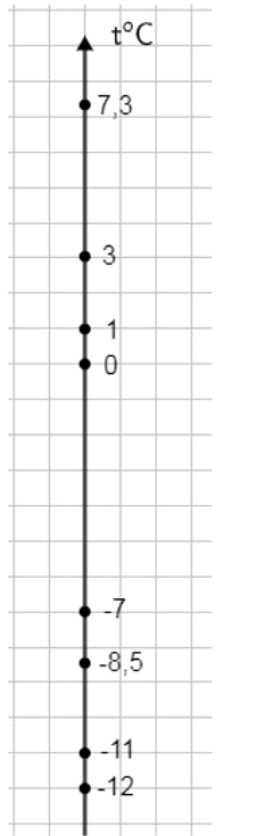
Изобразите вертикальную координатную прямую, обозначьте её \(t, ℃\) и отметьте на ней числа, соответствующие температуре: \(-12 ℃\); \(-11 ℃\); \(-7 ℃\); \(+3 ℃\); \(-8,5 ℃\); \(+7,3 ℃\).

а) Строим вертикальную ось \(t,\,^\circ C\) с нулем посередине и равным единичным шагом. Отрицательные значения размещаем ниже \(0^\circ C\), положительные — выше, дробные точки ставим пропорционально доле шага.

б) Наносим точки: ниже нуля ставим \(-12^\circ C\), \(-11^\circ C\), \(-8{,}5^\circ C\) (между \(-9^\circ C\) и \(-8^\circ C\) на \(\frac{1}{2}\) шага), \(-7^\circ C\); на нуле отмечаем \(0^\circ C\); выше нуля — \(+1^\circ C\), \(+3^\circ C\), \(+7{,}3^\circ C\) (на \(7\) шагах и ещё на \(\frac{3}{10}\) шага до \(8^\circ C\)).

в) Проверка порядка снизу вверх по возрастанию: \(-12^\circ C< -11^\circ C< -8{,}5^\circ C< -7^\circ C< 0^\circ C< +1^\circ C< +3^\circ C< +7{,}3^\circ C\). Дробные координаты выставлены долями единичного отрезка: \(0{,}5=\frac{1}{2}\), \(0{,}3=\frac{3}{10}\).

а) Строим вертикальную координатную прямую, направленную вверх, и обозначаем ось как \(t,\,^\circ C\). Точку отсчета принимаем в нуле: отметка \(0^\circ C\) делит ось на положительную (выше) и отрицательную (ниже) части. Единичный отрезок выбираем равномерным, чтобы каждое целое число градусов соответствовало равному шагу вверх или вниз. Это позволит корректно разместить как целые температуры, так и десятичные, используя доли единичного отрезка.

б) Наносим отрицательные температуры ниже нуля по мере убывания. Сначала ставим \(-12^\circ C\) как самую низкую точку; на один шаг выше располагаем \(-11^\circ C\). Далее между \(-9^\circ C\) и \(-8^\circ C\) на расстоянии \(\frac{1}{2}\) единичного шага отмечаем \(-8{,}5^\circ C\), то есть на середине между соответствующими целыми делениями. Еще выше, на целое деление, ставим \(-7^\circ C\). Каждая из этих точек подписывается слева или справа от оси значением температуры с сохранением знака минус, чтобы подчеркнуть их положение ниже уровня \(0^\circ C\).

в) Наносим неотрицательные температуры на верхней части оси. На отметке \(0^\circ C\) ставим точку нуля как границу между минусовыми и плюсовыми значениями. Затем выше на одно деление отмечаем \(+1^\circ C\), еще на два деления выше фиксируем \(+3^\circ C\). Для десятичной положительной температуры \(+7{,}3^\circ C\) поднимаемся на семь целых делений и добавляем \(0{,}3\) единичного шага, то есть \( \frac{3}{10} \) от расстояния между \(7^\circ C\) и \(8^\circ C\); точка будет немного ниже отметки \(8^\circ C\). Все положительные значения подписываем с плюсом или без знака, подчеркивая, что они расположены выше нуля.

г) Проверяем порядок размещения точек по возрастанию температуры вдоль оси снизу вверх: \(-12^\circ C\), \(-11^\circ C\), \(-8{,}5^\circ C\), \(-7^\circ C\), \(0^\circ C\), \(+1^\circ C\), \(+3^\circ C\), \(+7{,}3^\circ C\). Такой порядок согласован с правилом: если \(a<b\), то на вертикальной оси точка \(a\) находится ниже точки \(b\). Десятичные значения размещаются пропорционально части единичного отрезка, например \(0{,}5=\frac{1}{2}\) для \(-8{,}5^\circ C\) и \(0{,}3=\frac{3}{10}\) для \(+7{,}3^\circ C\).

д) Итог: на оси \(t\) в градусах Цельсия корректно отмечены температуры \(-12^\circ C\), \(-11^\circ C\), \(-8{,}5^\circ C\), \(-7^\circ C\), \(0^\circ C\), \(+1^\circ C\), \(+3^\circ C\), \(+7{,}3^\circ C\), что полностью соответствует требуемой разметке и отражает правильное расположение отрицательных и положительных значений относительно нуля.