ГДЗ по Математике 6 Класс Часть 2 Номер 4.151 Виленкин, Жохов — Подробные Ответы

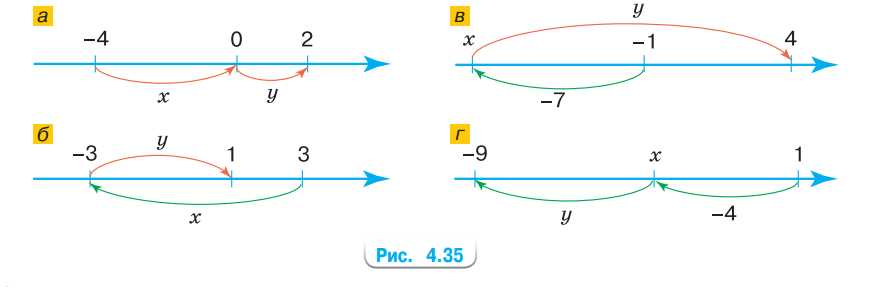
По схеме на рисунке 4.35 найдите значения \(x\) и \(y\). 

а) Решаем уравнения:
\(-4 + x = 0 \Rightarrow x = 4\);
\(0 + y = 2 \Rightarrow y = 2\).
Ответ: \(x = 4\), \(y = 2\).

б) Решаем уравнения:
\(3 + x = -3 \Rightarrow x = -3 — 3 \Rightarrow x = -6\);
\(-3 + y = 1 \Rightarrow y = 1 + 3 \Rightarrow y = 4\).
Ответ: \(x = -6\), \(y = 4\).

в) Решаем уравнения:
\(-1 — 7 = x \Rightarrow x = -8\);
\(-8 + y = 4 \Rightarrow y = 4 + 8 \Rightarrow y = 12\).
Ответ: \(x = -8\), \(y = 12\).

г) Решаем уравнения:
\(1 — 4 = x \Rightarrow x = -3\);
\(-3 + y = -9 \Rightarrow y = -9 + 3 \Rightarrow y = -6\).
Ответ: \(x = -3\), \(y = -6\).

1) Рассмотрим уравнение \(-4 + x = 0\). Чтобы найти \(x\), нужно избавиться от числа \(-4\), которое стоит слева. Для этого прибавим \(4\) к обеим частям уравнения, получим \(x = 0 + 4\), то есть \(x = 4\). Это значит, что при \(x = 4\) уравнение становится равенством. Аналогично, во втором уравнении \(0 + y = 2\) просто \(y = 2\), так как \(0\) не влияет на сумму. Таким образом, решения для переменных: \(x = 4\), \(y = 2\).

2) Во втором примере уравнение \(3 + x = -3\) требует найти число \(x\), которое при сложении с \(3\) даст \(-3\). Чтобы изолировать \(x\), вычтем \(3\) из обеих частей уравнения: \(x = -3 — 3\), что равно \(x = -6\). Во втором уравнении \(-3 + y = 1\) необходимо найти \(y\), для этого прибавим \(3\) к обеим частям: \(y = 1 + 3\), значит \(y = 4\). Итог: \(x = -6\), \(y = 4\).

3) В третьем случае уравнение \(-1 — 7 = x\) можно упростить, сложив числа слева: \(-1 — 7 = -8\), значит \(x = -8\). Следующее уравнение \(-8 + y = 4\) требует найти \(y\). Прибавим \(8\) к обеим частям: \(y = 4 + 8\), отсюда \(y = 12\). Получаем \(x = -8\), \(y = 12\).

4) В последнем примере уравнение \(1 — 4 = x\) упрощается до \(x = -3\), так как \(1 — 4 = -3\). Второе уравнение \(-3 + y = -9\) решается прибавлением \(3\) к обеим частям: \(y = -9 + 3\), значит \(y = -6\). Ответ: \(x = -3\), \(y = -6\).