
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 4.137 Виленкин, Жохов — Подробные Ответы
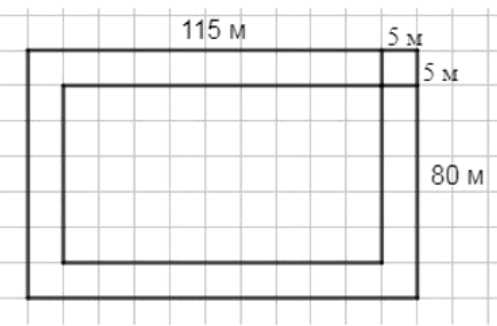
Под строительство спортивной площадки отвели поле прямоугольной формы площадью 9200 м² и шириной 80 м. По периметру поля планируется сделать беговые дорожки шириной 5 м, а в центральной части — футбольное поле. Найдите периметр и площадь футбольного поля.
Длина спортивной площадки: \( 9200 : 80 = 920 : 8 = 115 \) (м).
Длина футбольного поля: \( 115 — 5 \cdot 2 = 115 — 10 = 105 \) (м).
Ширина футбольного поля: \( 80 — 5 \cdot 2 = 80 — 10 = 70 \) (м).
Периметр футбольного поля: \( 2 \cdot (105 + 70) = 2 \cdot 175 = 350 \) (м).
Площадь футбольного поля: \( 105 \cdot 70 = 7350 \) (м²).
Ответ: \( 350 \) м; \( 7350 \) м².
1) Для начала вычислим длину всей спортивной площадки. Из условия известно, что площадь площадки равна 9200 м², а ширина — 80 м. Чтобы найти длину, нужно площадь разделить на ширину: \( \frac{9200}{80} = 115 \) м. В решении показано, что сначала 9200 делят на 80, а затем 920 делят на 8, что эквивалентно тому же действию, так как \( 9200 : 80 = 920 : 8 \). Таким образом, длина спортивной площадки равна 115 м.
2) Теперь найдем длину футбольного поля, которое находится внутри площадки и отстоит от краев на 5 м с каждой стороны. Значит, с каждой стороны длина уменьшается на 5 м дважды, то есть на \( 5 \cdot 2 = 10 \) м. Тогда длина поля будет равна \( 115 — 10 = 105 \) м. Это учитывает отступы по обеим сторонам.
3) Аналогично вычислим ширину футбольного поля. Исходная ширина площадки — 80 м, отступы по обеим сторонам также по 5 м, то есть суммарно 10 м. Значит, ширина поля равна \( 80 — 10 = 70 \) м. Таким образом, мы получили размеры футбольного поля: длина 105 м и ширина 70 м.
4) Следующий шаг — вычислить периметр футбольного поля. Периметр прямоугольника равен удвоенной сумме длины и ширины: \( 2 \cdot (105 + 70) = 2 \cdot 175 = 350 \) м. Это показывает, сколько метров составляет общий контур футбольного поля.
5) Наконец, вычислим площадь футбольного поля. Площадь прямоугольника равна произведению длины на ширину, то есть \( 105 \cdot 70 = 7350 \) м². Это количество квадратных метров, занимаемых футбольным полем внутри спортивной площадки.
Ответ: периметр футбольного поля равен \( 350 \) м, площадь — \( 7350 \) м².
| Величина | Формула | Результат |
|---|---|---|
| Длина спортивной площадки | \( \frac{9200}{80} \) | 115 м |
| Длина футбольного поля | \( 115 — 5 \cdot 2 \) | 105 м |
| Ширина футбольного поля | \( 80 — 5 \cdot 2 \) | 70 м |
| Периметр футбольного поля | \( 2 \cdot (105 + 70) \) | 350 м |
| Площадь футбольного поля | \( 105 \cdot 70 \) | 7350 м2 |

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!