
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 4.130 Виленкин, Жохов — Подробные Ответы
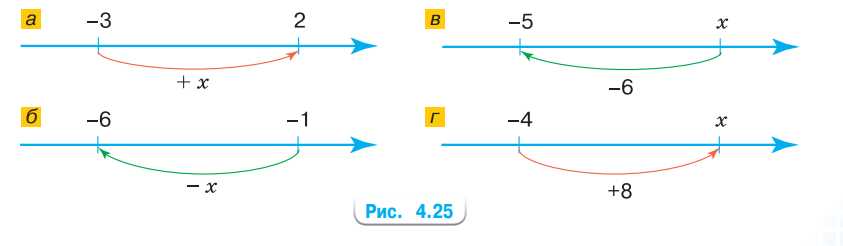
С помощью рисунка 4.25 найдите значение \(x\).
а) Уравнение \( -3 + x = 2 \). Переносим \(-3\) вправо: \( x = 2 + 3 \). Получаем \( x = 5 \).
б) Уравнение \( -1 — x = -6 \). Переносим \(-1\) вправо: \( -x = -6 + 1 \), или \( -x = -5 \). Умножаем на \(-1\): \( x = 5 \).
в) Уравнение \( x — 6 = -5 \). Переносим \(-6\) вправо: \( x = -5 + 6 \). Получаем \( x = 1 \).
г) Уравнение \( -4 + 8 = x \). Считаем левую часть: \( 4 = x \). Ответ: \( x = 4 \).
а) Рассмотрим уравнение \( -3 + x = 2 \). Здесь нам нужно найти значение \( x \), при котором выражение слева равно числу 2. Чтобы изолировать \( x \), нужно избавиться от числа \(-3\), которое находится слева. Для этого прибавим 3 к обеим частям уравнения, так как прибавление одинакового числа к обеим частям уравнения не изменяет его равенства. Получаем: \( -3 + x + 3 = 2 + 3 \). Левая часть упрощается, так как \(-3 + 3 = 0\), и остаётся только \( x \). Правая часть равна \( 5 \). Значит, \( x = 5 \).
Таким образом, мы получили, что при \( x = 5 \) исходное уравнение становится верным: \( -3 + 5 = 2 \), что действительно так, так как \( 2 = 2 \). Это подтверждает правильность решения. Ответ записываем как \( x = 5 \).
б) Уравнение \( -1 — x = -6 \) требует найти \( x \). Сначала перенесём число \(-1\) вправо, чтобы оставить только \( -x \) слева. Для этого прибавим 1 к обеим частям уравнения: \( -1 — x + 1 = -6 + 1 \). Левая часть упрощается до \( -x \), правая — до \(-5\). Теперь у нас есть \( -x = -5 \). Чтобы найти \( x \), умножим обе части уравнения на \(-1\), меняя знак: \( x = 5 \).
Проверим: подставим \( x = 5 \) в исходное уравнение: \( -1 — 5 = -6 \). Левая часть равна \(-6\), что совпадает с правой, значит решение верно. Ответ: \( x = 5 \).
в) Рассмотрим уравнение \( x — 6 = -5 \). Чтобы найти \( x \), нужно избавиться от числа \(-6\), стоящего слева. Для этого прибавим 6 к обеим частям уравнения: \( x — 6 + 6 = -5 + 6 \). Левая часть упрощается до \( x \), правая — до \( 1 \). Значит, \( x = 1 \).
Проверка: подставим \( x = 1 \) в исходное уравнение, получим \( 1 — 6 = -5 \), что верно. Ответ: \( x = 1 \).
г) В уравнении \( -4 + 8 = x \) сначала вычислим левую часть. \( -4 + 8 = 4 \). Значит, \( x = 4 \). Здесь переменная уже изолирована, и осталось только посчитать числовое выражение. Ответ: \( x = 4 \).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!