
ДЗ к учебнику Виленкина, Жохова, Чеснокова за 6 класс, часть 2 — это продолжение базовой линии курса, где уже отрабатываются навыки вычислений и решаются более прикладные задачи. Во второй части появляется системность: темы связываются между собой, а решения требуют аккуратности на каждом шаге. Решебник здесь помогает не просто сверить итог, а восстановить логику — увидеть, почему именно так выбирается способ, как обосновывается переход между действиями и где чаще всего возникают ошибки.
ГДЗ по Математике 6 Класс Часть 2 Номер 4.129 Виленкин, Жохов — Подробные Ответы
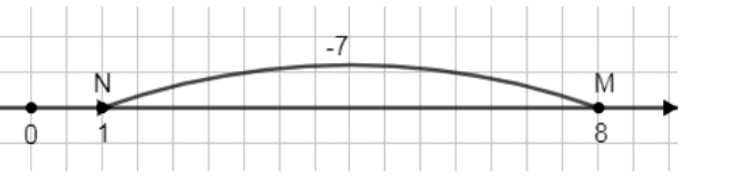
На сколько единиц должна переместиться точка \(M(8)\) по координатной прямой, чтобы попасть:
а) в точку \(N(1)\);
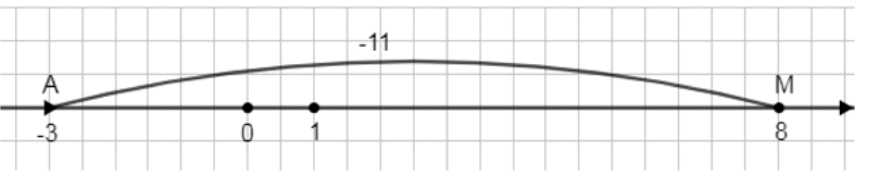
б) в точку \(A(-3)\)?
а) Чтобы точка \( M(8) \) попала в точку \( N(1) \), нужно переместить её на \( 1 — 8 = -7 \) единиц.
б) Чтобы точка \( M(8) \) попала в точку \( A(-3) \), нужно переместить её на \( -3 — 8 = -11 \) единиц.
1) Чтобы понять, на сколько единиц нужно переместить точку \( M \) с координатой 8, чтобы она попала в точку \( N \) с координатой 1, необходимо вычислить разницу между координатами этих точек. Перемещение точки по числовой оси определяется вычитанием координаты начальной точки из координаты конечной. В данном случае вычисляем: \( 1 — 8 = -7 \). Это означает, что точку \( M \) нужно сдвинуть на 7 единиц влево, то есть в отрицательном направлении, чтобы она совпала с точкой \( N \).
2) Аналогично для точки \( M \), чтобы попасть в точку \( A \) с координатой -3, нужно определить величину смещения. Вычисляем разницу координат: \( -3 — 8 = -11 \). Это указывает на то, что точку \( M \) нужно переместить на 11 единиц влево по числовой оси. Отрицательное значение смещения говорит о движении в сторону уменьшения координат, что соответствует направлению влево на оси.
В обоих случаях перемещение точки \( M \) сводится к вычислению разности координат конечной и начальной точек. Отрицательный знак результата указывает на направление перемещения — влево. Таким образом, для попадания точки \( M(8) \) в точку \( N(1) \) нужно переместить её на \( -7 \) единиц, а для попадания в точку \( A(-3) \) — на \( -11 \) единиц. Это простой и наглядный способ определить необходимое смещение на числовой оси.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!