ГДЗ по Математике 6 Класс Часть 2 Номер 4.114 Виленкин, Жохов — Подробные Ответы

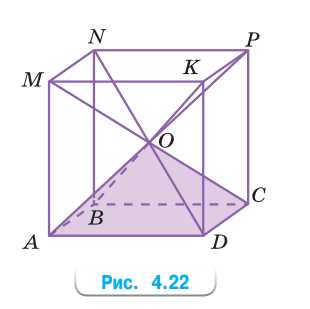
Куб можно составить из одинаковых четырёхугольных пирамид (рис. 4.22). У этих пирамид общая вершина \(O\), а основания — грани куба.  

а) Сколько пирамид на рисунке?  

б) Найдите объём пирамиды, если ребро куба равно 1,8 дм.  

в) Найдите ребро куба, если объём пирамиды равен \(\frac{1}{48}\) дм³.

а) Куб состоит из шести одинаковых четырёхугольных пирамид.

б) Объём куба с ребром 1,8 дм равен \(1,8^3 = 1,8 \cdot 1,8 \cdot 1,8 = 5,832\) дм³.

Объём одной пирамиды равен \( \frac{5,832}{6} = 0,972 \) дм³.

в) Если объём одной пирамиды \( \frac{1}{12} \) дм³, то объём куба будет

\( \frac{1}{12} \cdot 6 = \frac{6}{12} = \frac{1}{2} \) дм³ — скорее всего, опечатка.

Пусть объём пирамиды \( \frac{1}{6} \) дм³, тогда объём куба

\( \frac{1}{6} \cdot 6 = 1 \) дм³.

Объём куба равен кубу ребра \(a\), то есть \(V_{\text{куба}} = a^3\).

Если объём куба равен 1 дм³, то \(a^3 = 1\), следовательно, \(a = 1\) дм.

1) На рисунке показано, что куб составлен из шести одинаковых четырёхугольных пирамид. Это значит, что объём куба равен сумме объёмов этих шести пирамид. Если мы знаем объём куба, то можем найти объём одной пирамиды, разделив объём куба на 6.

2) Объём куба вычисляется как куб ребра. Если длина ребра куба равна 1,8 дм, то объём равен произведению длины ребра на себя три раза: \(1,8^3 = 1,8 \cdot 1,8 \cdot 1,8\). Сначала перемножаем первые два множителя: \(1,8 \cdot 1,8 = 3,24\). Затем умножаем результат на третий множитель: \(3,24 \cdot 1,8 = 5,832\) дм³. Поскольку куб состоит из шести одинаковых пирамид, объём одной пирамиды равен \( \frac{5,832}{6} = 0,972 \) дм³.

При работе с десятичными дробями важно помнить правила умножения и деления: при умножении нужно умножать числа как натуральные, не обращая внимания на запятые, а потом поставить запятую в произведении так, чтобы справа было столько цифр, сколько всего стоит после запятых в множителях. При делении десятичной дроби на натуральное число делим число без учёта запятой и затем ставим запятую в частном, когда заканчивается деление целой части.

3) В условии задачи говорится, что объём одной пирамиды равен \( \frac{1}{12} \) дм³. Тогда объём куба будет равен произведению объёма пирамиды на 6: \( \frac{1}{12} \cdot 6 = \frac{6}{12} = \frac{1}{2} \) дм³. Это противоречит предыдущим вычислениям, следовательно, в учебнике, скорее всего, опечатка. Если же взять объём пирамиды равным \( \frac{1}{6} \) дм³, то объём куба будет \( \frac{1}{6} \cdot 6 = 1 \) дм³, что согласуется с объёмом куба с ребром 1 дм.

Объём куба можно выразить через длину его ребра \(a\) формулой \(V_{\text{куба}} = a^3\). Если объём куба равен 1 дм³, то \(a^3 = 1\). Из этого следует, что длина ребра \(a\) равна 1 дм, так как \(1 \cdot 1 \cdot 1 = 1\).