ГДЗ по Математике 6 Класс Часть 2 Номер 4.105 Виленкин, Жохов — Подробные Ответы

На координатной прямой отмечены две точки:  

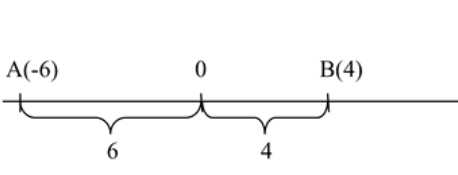
а) \(A(-6)\) и \(B(4)\);  

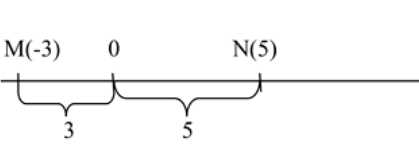
б) \(M(-3)\) и \(N(5)\).  

Какое расстояние между точками и какая из точек расположена дальше от начала отсчёта?

а) \(AB=|-6-4|=|-10|=10\). Удалённость от нуля: \(|-6|=6\), \(|4|=4\), значит дальше от нуля точка \(A\).

б) \(MN=|-3-5|=|-8|=8\). Удалённость от нуля: \(|-3|=3\), \(|5|=5\), значит дальше от нуля точка \(N\).

1) Для точек \(A(-6)\) и \(B(4)\) расстояние на числовой прямой вычисляется как модуль разности координат: \(AB=|x_{A}-x_{B}|\). Подставляя значения, получаем \(AB=|-6-4|=|-10|=10\). Это означает, что между числами \(-6\) и \(4\) на числовой прямой расположено ровно 10 единичных отрезков. Чтобы понять, какая точка дальше от начала отсчёта, сравним расстояния каждой точки до нуля, то есть значения модулей их координат: \(|-6|=6\) и \(|4|=4\). Так как \(6>4\), точка \(A\) расположена дальше от нуля, чем точка \(B\). Здесь важно помнить, что модуль показывает именно расстояние, поэтому знак числа не влияет на результат: отрицательные и положительные числа одинаково учитываются по удалённости от нуля через модуль.

2) Для точек \(M(-3)\) и \(N(5)\) применяем ту же формулу расстояния: \(MN=|x_{M}-x_{N}|\). Подставим координаты: \(MN=|-3-5|=|-8|=8\). Следовательно, между числами \(-3\) и \(5\) на числовой прямой 8 единичных отрезков. Для определения, какая из точек дальше от начала отсчёта, снова сравниваем значения модулей их координат: \(|-3|=3\) и \(|5|=5\). Так как \(3<5\), точка \(N\) удалена от нуля больше, чем точка \(M\). Это логично: хотя \(-3\) меньше \(5\) как число, при измерении расстояний учитывается только величина без знака, и число с большей абсолютной величиной находится дальше от нуля.

Дополнительные пояснения. Формула расстояния между двумя точками на числовой прямой \(x\) и \(y\) записывается как \(d=|x-y|\). Эта запись гарантирует неотрицательный результат, поскольку расстояние не может быть отрицательным. В пункте 1) мы получили \(-10\) как разность координат, но модуль преобразовал его в \(10\); в пункте 2) аналогично \(-8\) преобразовалось в \(8\). Для сравнения удалённости от начала координат используется модуль каждой координаты: если \(|x_{1}|>|x_{2}|\), то точка с координатой \(x_{1}\) дальше от нуля. Поэтому в первом случае \(|-6|=6\) больше, чем \(|4|=4\), а во втором \(|5|=5\) больше, чем \(|-3|=3\).