
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Применяем математику Параграф 3 Номер 6 Виленкин, Жохов — Подробные Ответы
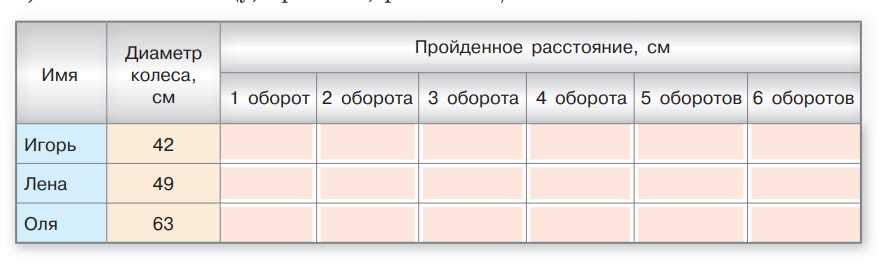
В таблице указаны диаметры колёс велосипедов, на которых катаются Игорь, Лена и Оля.
1) Заполните таблицу, приняв \(\pi\), равным \(22/7\).
2) Определите:
а) кто из детей проедет дальше и на сколько, если колёса их велосипедов сделали четыре полных оборота;
б) сколько полных оборотов должны сделать колёса велосипеда Оли, чтобы проехать 990 см.
3) Лена может ездить на трёх скоростях, которые устанавливаются с помощью нижней, средней и верхней передач. У её велосипеда следующие передаточные соотношения: нижнее — \(3:1\), среднее — \(6:5\) и верхнее — \(1:2\). Сколько раз Лене надо повернуть педали, чтобы проехать 600 м на средней передаче?
Примечание. Передаточное соотношение \(3:1\) означает, что при трёх полных поворотах педалей колесо велосипеда делает один полный оборот.
а) Оля проедет дальше всех за 4 полных оборота, на \( 792 — 528 = 264 \) см дальше Игоря и на \( 792 — 616 = 176 \) см дальше Лены.
б) Чтобы проехать \( 990 \) см, колеса Оли должны сделать пять полных оборотов.
1. Лене нужно сделать \( \frac{60000}{154} \approx 389,61 = 390 \) полных оборотов, чтобы проехать \( 600 \) м.
2. Чтобы проехать \( 600 \) м, Лене нужно повернуть педали \( x \) раз.
3. Составим пропорцию: \( \frac{x}{390} = \frac{6}{5} \), решив уравнение получим \( 5x = 390 \times 6 \), \( x = \frac{390 \times 6}{5} = 468 \) поворотов педалей.
| Имя | Диаметр колеса, см | Пройденное расстояние, см | 1 оборот | 2 оборота | 3 оборота | 4 оборота | 5 оборотов | 6 оборотов |
|---|---|---|---|---|---|---|---|---|
| Игорь | 42 | 132 | 132 | 264 | 396 | 528 | 660 | 792 |
| Лена | 49 | 154 | 154 | 308 | 462 | 616 | 770 | 924 |
| Оля | 63 | 198 | 198 | 396 | 594 | 792 | 990 | 1188 |
а) Оля проедет дальше всех за 4 полных оборота, на \( 792 — 528 = 264 \) см дальше Игоря и на \( 792 — 616 = 176 \) см дальше Лены. Это происходит потому, что диаметр колеса Оли больше, чем у Игоря и Лены, и поэтому за один оборот она проезжает большее расстояние. Расстояние, пройденное Олей за 4 оборота, можно рассчитать по формуле \( 4 \times 198 = 792 \) см, где \( 198 \) см — расстояние, пройденное Олей за один оборот. Аналогично, расстояние, пройденное Игорем за 4 оборота, равно \( 4 \times 132 = 528 \) см, а расстояние, пройденное Леной за 4 оборота, равно \( 4 \times 154 = 616 \) см.
б) Чтобы проехать \( 990 \) см, колеса Оли должны сделать пять полных оборотов. Это можно рассчитать по формуле \( 5 \times 198 = 990 \) см, где \( 198 \) см — расстояние, пройденное Олей за один оборот. Это означает, что Оле нужно сделать 5 оборотов, чтобы проехать \( 990 \) см. Для сравнения, Игорю нужно сделать \( \frac{990}{132} \approx 7,5 \) оборотов, чтобы проехать то же расстояние, а Лене нужно сделать \( \frac{990}{154} \approx 6,4 \) оборотов.
1. Лене нужно сделать \( \frac{60000}{154} \approx 389,61 = 390 \) полных оборотов, чтобы проехать \( 600 \) м. Это можно рассчитать по формуле \( \frac{60000}{154} \), где \( 60000 \) — расстояние в сантиметрах, которое нужно проехать, а \( 154 \) — расстояние, пройденное Леной за один оборот. Это означает, что Лене нужно сделать 390 оборотов, чтобы проехать \( 600 \) м.
2. Чтобы проехать \( 600 \) м, Лене нужно повернуть педали \( x \) раз. Это можно рассчитать по формуле \( \frac{x}{390} = \frac{6}{5} \), где \( x \) — количество раз, которое нужно повернуть педали, а \( 390 \) — количество оборотов, которое нужно сделать, чтобы проехать \( 600 \) м. Решив уравнение, получим \( 5x = 390 \times 6 \), \( x = \frac{390 \times 6}{5} = 468 \) поворотов педалей.
3. Составим пропорцию: \( \frac{x}{390} = \frac{6}{5} \), решив уравнение получим \( 5x = 390 \times 6 \), \( x = \frac{390 \times 6}{5} = 468 \) поворотов педалей. Это означает, что Лене нужно повернуть педали 468 раз, чтобы проехать \( 600 \) м.
| Имя | Диаметр колеса, см | Пройденное расстояние, см | 1 оборот | 2 оборота | 3 оборота | 4 оборота | 5 оборотов | 6 оборотов |
|---|---|---|---|---|---|---|---|---|
| Игорь | 42 | 132 | 132 | 264 | 396 | 528 | 660 | 792 |
| Лена | 49 | 154 | 154 | 308 | 462 | 616 | 770 | 924 |
| Оля | 63 | 198 | 198 | 396 | 594 | 792 | 990 | 1188 |
Для расчета количества оборотов, которое нужно сделать каждому человеку, чтобы проехать определенное расстояние, можно использовать формулу \( \frac{расстояние}{расстояние за один оборот} \). Например, чтобы рассчитать, сколько оборотов нужно сделать Игорю, чтобы проехать \( 600 \) м, можно использовать формулу \( \frac{60000}{132} \approx 454,5 \) оборотов. Аналогично, чтобы рассчитать, сколько оборотов нужно сделать Лене, чтобы проехать \( 600 \) м, можно использовать формулу \( \frac{60000}{154} \approx 389,6 \) оборотов. Это означает, что Игорю нужно сделать примерно 454,5 оборота, а Лене нужно сделать примерно 389,6 оборотов, чтобы проехать \( 600 \) м.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!