ГДЗ по Математике 6 Класс Часть 1 Применяем математику Параграф 1 Номер 7 Виленкин, Жохов — Подробные Ответы

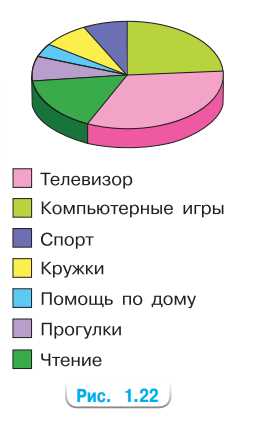
1) На круговой диаграмме (рис. 1.22) показано использование свободного времени за неделю шестиклассником Димой.

Определите:
а) на что он тратит меньше всего времени;
б) сколько процентов свободного времени Дима тратит на компьютерные игры.
2) Нужно ли что-то изменить Диме в распределении свободного времени?
3) Составьте диаграмму использования своего свободного времени за неделю и проанализируйте её.

1) а) Меньше всего времени — помощь по дому.
б) Сектор «Компьютерные игры» — четверть круга, значит \(25\%\) свободного времени.

2) Да. Стоит сократить время на телевизор и компьютерные игры и увеличить долю спорта, прогулок и чтения, так полезнее для здоровья и развития.

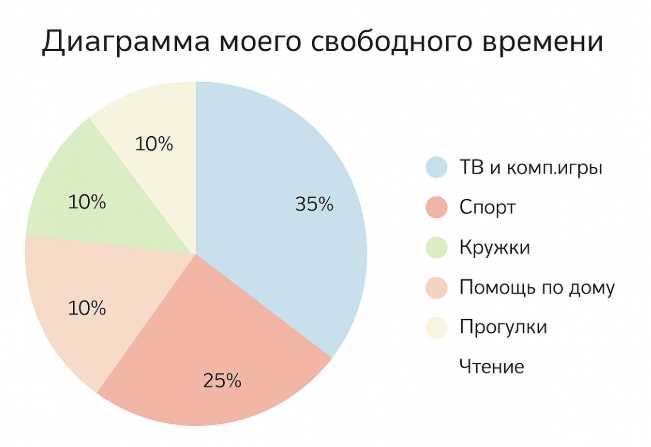
3) Пример моей диаграммы (кратко):

— ТВ и компьютерные игры — \(20\%\).
— Спорт — \(25\%\).
— Кружки — \(15\%\).
— Помощь по дому — \(10\%\).
— Прогулки — \(15\%\).
— Чтение — \(15\%\).
Проверка: \(20+25+15+10+15+15=100\%\). Баланс смещён в пользу активностей и чтения; время за экраном ограничено до \(20\%\).

1) а) На круговой диаграмме каждый сектор показывает долю времени за неделю. Самый маленький сектор — «Помощь по дому». Следовательно, именно на домашние дела Дима тратит наименьшую часть свободного времени. Это видно визуально: угол и площадь этого сектора минимальны относительно остальных, что по свойствам круговой диаграммы означает наименьший процент. б) Сектор «Компьютерные игры» по размеру равен четверти круга: его центральный угол примерно \( \frac{1}{4} \) полного угла круга. Полный круг — \(360^{\circ}\), тогда угол сектора около \( \frac{1}{4}\cdot 360^{\circ}=90^{\circ} \). Процентная доля рассчитывается по формуле \(p=\frac{\text{угол сектора}}{360^{\circ}}\cdot 100\%\). Подставляя, получаем \(p=\frac{90^{\circ}}{360^{\circ}}\cdot 100\%=25\%\). Итак, на компьютерные игры Дима тратит \(25\%\) свободного времени.

2) Диаграмма показывает значительную долю пассивных экранных активностей: «Телевизор» и «Компьютерные игры» вместе занимают большую часть круга. Для здоровья и развития школьника стоит перераспределить баланс, сократив экранное время и увеличив активные и развивающие занятия. Рациональная рекомендация: уменьшить телевизор и игры минимум на \(10\text{–}15\%\) совокупно, а высвобождённое время распределить между спортом, прогулками и чтением. Такой сдвиг улучшит физическую активность, зрение и качество сна, а также повысит учебную мотивацию и концентрацию. Минимальная практическая цель — придерживаться правила: не более \( \frac{1}{5} = 20\% \) свободного времени на экранные развлечения в будни и немного больше в выходные при условии компенсации спортом и отдыхом на свежем воздухе.

3) Пример моей диаграммы с проверкой баланса и анализом.

Предлагаемое распределение на неделю: ТВ и компьютерные игры — \(20\%\); спорт — \(25\%\); кружки — \(15\%\); помощь по дому — \(10\%\); прогулки — \(15\%\); чтение — \(15\%\). Сумма процентов обязана равняться \(100\%\): \(20+25+15+10+15+15=100\%\), что проверяет корректность. В таком плане доля активностей на свежем воздухе и двигательной нагрузки равна \(25\%+15\%=40\%\), доля развития навыков и когнитивной нагрузки равна \(15\%+15\%=30\%\), бытовые обязанности занимают \(10\%\), а экранное развлечение ограничено \(20\%\). Это распределение делает структуру недели устойчивой: есть ежедневное движение, развитие интересов, чтение для расширения кругозора и умеренное время у экрана, что снижает переутомление и поддерживает здоровье.