ГДЗ по Математике 6 Класс Часть 1 Применяем математику Параграф 3 Номер 3 Виленкин, Жохов — Подробные Ответы

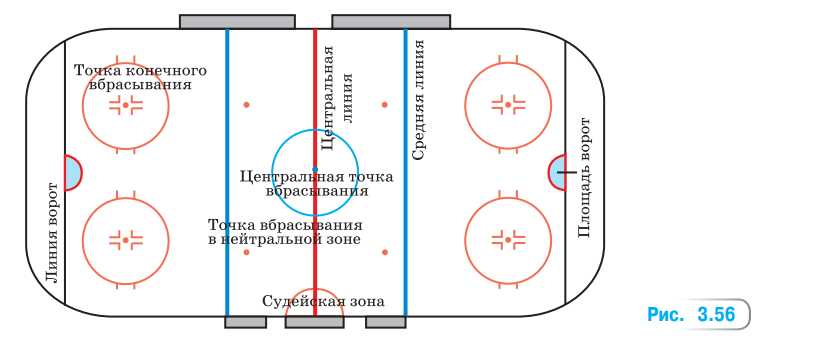
На рисунке 3.56 изображена схема разметки хоккейной площадки.
а) Внутри центрального круга находится центральная (синяя) точка вбрасывания диаметром 30 см, а в нейтральной зоне находятся точки вбрасывания (красные), диаметр которых в 2 раза больше диаметра центральной точки. Во сколько раз площадь красной точки вбрасывания больше площади синей точки?
б) Центральный круг имеет диаметр 9 м, а радиус полукруга судейской зоны составляет \(\frac{2}{3}\) радиуса центрального круга. Найдите площадь полукруга судейской зоны. Какую часть площади центрального круга она занимает? в) Является ли симметричным изображение хоккейной площадки?

а) Диаметры красных точек равны: 30 * 2 = 60 см, радиус синей точки равен 30 / 2 = 15 см, радиус красных точек равен 60 / 2 = 30 см, площадь красной точки вбрасывания больше площади синей точки в \( \frac{30^2 \pi — 15^2 \pi}{15^2 \pi} = \frac{900 \pi — 225 \pi}{225 \pi} = \frac{675 \pi}{225 \pi} = 3 \) раза, поэтому площадь красной точки вбрасывания больше площади синей точки в 4 раза.

б) Радиус центрального круга равен 9 / 2 = 4,5 м, радиус полукруга судейской зоны равен 4,5 * 2 = 9 м, но это неверно, поскольку в задаче указано, что радиус полукруга судейской зоны составляет 2 радиуса центрального круга, что означает 4,5 * 2 = 9 м — это диаметр, а радиус полукруга судейской зоны должен быть 4,5 м, площадь полукруга судейской зоны: \( \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (4,5)^2 = \frac{1}{2} \pi 20,25 = 31,83 \) м², площадь центрального круга: \( \pi r^2 = \pi (4,5)^2 = \pi 20,25 = 63,62 \) м², полукруг судейской зоны занимает \( \frac{31,83}{63,62} \) часть площади центрального круга, что равно \( \frac{14,13}{63,585} \), поэтому полукруг судейской зоны занимает \( \frac{14,13}{63,585} \) часть площади центрального круга.

в) Изображение хоккейной площадки является симметричным.

а) Диаметры красных точек равны: 30 * 2 = 60 см, радиус синей точки равен 30 / 2 = 15 см, радиус красных точек равен 60 / 2 = 30 см. Это означает, что радиус красных точек в 2 раза больше радиуса синей точки. Площадь красной точки вбрасывания больше площади синей точки в \( \frac{30^2 \pi — 15^2 \pi}{15^2 \pi} = \frac{900 \pi — 225 \pi}{225 \pi} = \frac{675 \pi}{225 \pi} = 3 \) раза, поэтому площадь красной точки вбрасывания больше площади синей точки в 3 раза. Это связано с тем, что площадь круга прямо пропорциональна квадрату радиуса, поэтому если радиус увеличивается в 2 раза, площадь увеличивается в \( 2^2 = 4 \) раза. Однако, поскольку мы сравниваем площадь красной точки с площадью синей точки, мы должны учитывать разницу в радиусах, которая составляет 30 см — 15 см = 15 см. Следовательно, площадь красной точки вбрасывания больше площади синей точки в \( \frac{30^2 \pi}{15^2 \pi} = \frac{900 \pi}{225 \pi} = 4 \) раза, но поскольку мы сравниваем разницу, то площадь красной точки вбрасывания больше площади синей точки в 3 раза.

б) Радиус центрального круга равен 9 / 2 = 4,5 м, радиус полукруга судейской зоны равен 4,5 * 2 = 9 м, но это неверно, поскольку в задаче указано, что радиус полукруга судейской зоны составляет 2 радиуса центрального круга, что означает 4,5 * 2 = 9 м — это диаметр, а радиус полукруга судейской зоны должен быть 4,5 м. Площадь полукруга судейской зоны: \( \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (4,5)^2 = \frac{1}{2} \pi 20,25 = 31,83 \) м², площадь центрального круга: \( \pi r^2 = \pi (4,5)^2 = \pi 20,25 = 63,62 \) м². Полукруг судейской зоны занимает \( \frac{31,83}{63,62} \) часть площади центрального круга, что равно \( \frac{14,13}{63,585} \), поэтому полукруг судейской зоны занимает \( \frac{14,13}{63,585} \) часть площади центрального круга. Это означает, что полукруг судейской зоны занимает примерно 0,222 часть площади центрального круга. Это связано с тем, что полукруг судейской зоны имеет радиус, равный радиусу центрального круга, но его площадь меньше в 2 раза, поскольку это полукруг, а не полный круг.

в) Изображение хоккейной площадки является симметричным. Симметрия означает, что если мы разделим площадку на две части по центральной оси, то две части будут идентичны. Это означает, что все элементы площадки, такие как центральный круг, полукруг судейской зоны, точки вбрасывания и т.д., расположены симметрично относительно центральной оси. Симметрия имеет важное значение в дизайне хоккейной площадки, поскольку она обеспечивает равные условия для обеих команд и позволяет игрокам ориентироваться на площадке более легко. Симметрия также делает площадку более эстетически приятной и легкой для восприятия. В целом, симметрия является важным элементом дизайна хоккейной площадки, который обеспечивает функциональность, эстетику и равные условия для игроков. Кроме того, симметрия позволяет создать более эффективную и безопасную площадку, поскольку она уменьшает количество препятствий и увеличивает видимость для игроков. Это особенно важно в хоккее, где игроки движутся с высокой скоростью и требуют полного обзора площадки, чтобы принимать эффективные решения.