
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Применяем математику Параграф 2 Номер 5 Виленкин, Жохов — Подробные Ответы
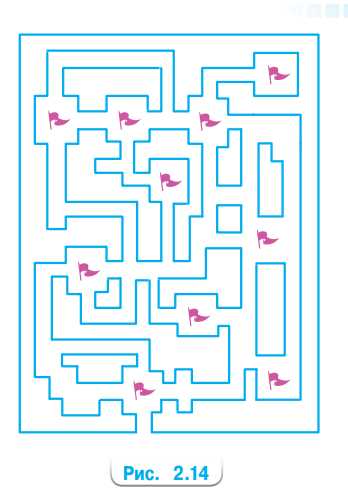
В небольшом городке 10 памятников архитектуры (рис. 2.14). Туристу хочется посетить их все, не проходя дважды по одной и той же улице. Может ли он это сделать?
Турист сможет посетить все памятники архитектуры, не проходя дважды по одной и той же улице, если маршрут образует эйлеров путь или эйлеров цикл в графе улиц.
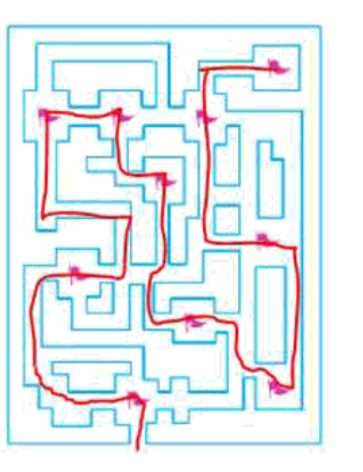
На изображении показан маршрут, который проходит по всем улицам ровно один раз, то есть это эйлеров путь.
Кратко:
Для существования такого маршрута в графе улиц должно быть не более двух вершин с нечётной степенью. Если таких вершин нет — существует эйлеров цикл, если две — существует эйлеров путь. Здесь маршрут соответствует условию, значит, граф удовлетворяет этим условиям.
1. Для того чтобы турист мог посетить все памятники архитектуры, не проходя дважды по одной и той же улице, необходимо, чтобы маршрут представлял собой эйлеров путь или эйлеров цикл в графе, где вершины — это перекрёстки, а рёбра — улицы. Эйлеров путь — это такой путь, который проходит по каждому ребру ровно один раз. Если такой путь начинается и заканчивается в одной и той же вершине, он называется эйлеровым циклом.
2. В теории графов существует важное условие для существования эйлерова пути: в графе должно быть не более двух вершин с нечётной степенью (числом рёбер, исходящих из вершины). Если все вершины имеют чётную степень, существует эйлеров цикл, то есть маршрут, начинающийся и заканчивающийся в одной точке, проходящий по всем улицам ровно один раз. Если ровно две вершины имеют нечётную степень, существует эйлеров путь, который начинается в одной из этих вершин и заканчивается в другой. Если же таких вершин больше двух, эйлеров путь невозможен.
3. На изображении показан маршрут, который проходит по всем улицам ровно один раз, не повторяя ни одну улицу дважды. Это означает, что граф улиц удовлетворяет условию о количестве вершин с нечётной степенью. Таким образом, турист может пройти по маршруту, который посещает все памятники архитектуры, не возвращаясь по тем же улицам. Это и есть эйлеров путь, подтверждающий, что поставленная задача решаема при данных условиях.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!