
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.83 Виленкин, Жохов — Подробные Ответы
Развивай память. Развить слуховую и зрительную память поможет пирамида из двузначных чисел. Числа в пирамиде могут быть другие.
а) Для проверки слуховой памяти попросите кого-нибудь прочитать числа из первой строки, после чего вы по памяти их записываете по порядку. Затем вторую строку и т. д. Если сможете без ошибок записать числа трёх строк, то слуховая память у вас хорошая, если больше, то отличная. Если допускаете ошибки при записи первых трёх строк, то меняйте числа и тренируйтесь.
б) При проверке зрительной памяти сначала закройте всю пирамиду, а затем на 5–15 с (в зависимости от количества чисел в строке) откройте первую строку и, закрыв её, по памяти запишите числа по порядку. Если записали числа правильно, переходите ко второй строке и т. д.
а) Для проверки слуховой памяти:
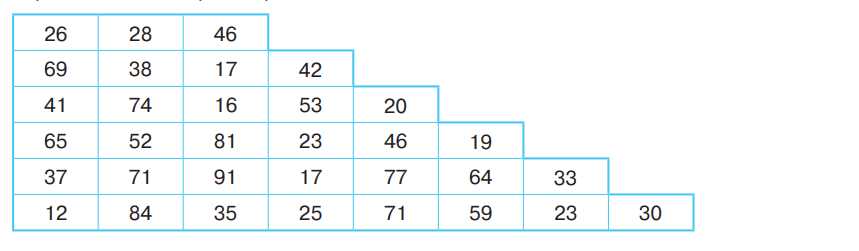
Попросите прочитать числа первой строки: 26, 28, 46. Запишите по памяти. Затем вторую строку: 69, 38, 17, 42. И так далее. Если сможете правильно записать три строки подряд — слуховая память хорошая, больше трёх — отличная. Если ошибки — меняйте числа и тренируйтесь.
б) Для проверки зрительной памяти:
Закройте пирамиду, откройте на 5–15 секунд первую строку (26, 28, 46), затем закройте и запишите по памяти. Если правильно, переходите ко второй строке (69, 38, 17, 42) и так далее.
Числа для тренировки:
| 26 | 28 | 46 | |||||
| 69 | 38 | 17 | 42 | ||||
| 41 | 74 | 16 | 53 | 20 | |||
| 65 | 52 | 81 | 23 | 46 | 19 | ||
| 37 | 71 | 91 | 17 | 77 | 64 | 33 | |
| 12 | 84 | 35 | 25 | 71 | 59 | 23 | 30 |
1. На координатном луче каждое из чисел \( p \), \( q \), \( m \), \( n \) соответствует определённому количеству равных частей. Из условия видно, что число \( p \) занимает одну такую часть, \( q \) — три часта) Для проверки слуховой памяти необходимо, чтобы кто-то вслух прочитал вам числа из первой строки пирамиды: 26, 28, 46. Ваша задача — внимательно слушать и затем записать эти числа по памяти в том же порядке. После этого попросите прочитать вторую строку: 69, 38, 17, 42, и снова запишите их по памяти. Продолжайте этот процесс, переходя к третьей строке и далее. Если вы сможете без ошибок воспроизвести три строки подряд, это свидетельствует о хорошем уровне слуховой памяти. Если же вы сможете правильно записать больше трёх строк, то ваша слуховая память считается отличной. В случае ошибок при записи первых трёх строк рекомендуется заменить числа и повторить тренировку, чтобы улучшить навыки запоминания.
б) При проверке зрительной памяти сначала закройте всю пирамиду, чтобы она была невидима. Затем откройте только первую строку на 5–15 секунд, в зависимости от количества чисел в строке (в данном случае три числа: 26, 28, 46). За это время внимательно запомните все числа. После этого закройте строку и попытайтесь воспроизвести её по памяти, записав числа в правильном порядке. Если вы сделали это без ошибок, переходите ко второй строке (69, 38, 17, 42) и повторите процесс. Постепенно переходите к последующим строкам, увеличивая объём информации для запоминания. Этот метод тренирует вашу зрительную память, развивает способность удерживать в голове визуальные образы.
Числа для тренировки представлены в виде пирамиды, где каждая строка содержит всё больше чисел:
| 26 | 28 | 46 | |||||
| 69 | 38 | 17 | 42 | ||||
| 41 | 74 | 16 | 53 | 20 | |||
| 65 | 52 | 81 | 23 | 46 | 19 | ||
| 37 | 71 | 91 | 17 | 77 | 64 | 33 | |
| 12 | 84 | 35 | 25 | 71 | 59 | 23 | 30 |
Такой подход позволяет постепенно увеличивать нагрузку на память, что способствует её развитию и улучшению.
Для лучшего результата рекомендуется повторять упражнения регулярно, меняя числа или порядок их предъявления. Это поможет избежать привыкания мозга к одной и той же последовательности и стимулирует активную работу памяти. При использовании формул или числовых последовательностей в других задачах можно применять аналогичный принцип постепенного усложнения для тренировки концентрации и запоминания.и, а \( n \) — двенадцать частей. Это значит, что весь отрезок от 0 до \( n \) разделён на 12 равных частей, и каждая из них — это единичный шаг, которым измеряются положения \( p \), \( q \), \( m \), \( n \).
2. Пропорция, связывающая эти точки, выражается формулой \(\frac{p}{q} = \frac{m}{n}\). Подставляя известные значения частей, получаем \(\frac{1}{3} = \frac{m}{12}\). Это уравнение говорит о том, что отношение количества частей, соответствующих \( p \) и \( q \), равно отношению количества частей, соответствующих \( m \) и \( n \). Чтобы найти неизвестное \( m \), нужно решить это уравнение.
3. Решение уравнения основано на свойстве пропорции: произведение крайних членов равно произведению средних. Здесь крайние члены — это 1 и 12, а средние — 3 и \( m \). Значит, \(1 \cdot 12 = 3 \cdot m\). Отсюда выразим \( m \) как \( m = \frac{12}{3} = 4\). Таким образом, число \( m \) занимает 4 части на координатном луче, что соответствует четырём равным сегментам между 0 и \( n \).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!