
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.6 Виленкин, Жохов — Подробные Ответы
Начертите прямоугольники, отношение сторон которых равно: а) \(2 : 1\); б) \(1 : 1\); в) \(2 : 3\). Как называется прямоугольник в случае б)?
а) Постройте прямоугольник, у которого длина в 2 раза больше ширины: например, \(6\text{ см}\) и \(3\text{ см}\). Отношение сторон \(6:3=2:1\).
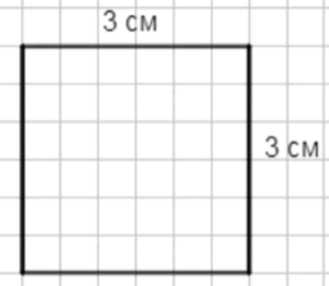
б) Постройте прямоугольник с равными сторонами: например, \(3\text{ см}\) и \(3\text{ см}\). Отношение сторон \(3:3=1:1\). Такой прямоугольник называется квадрат.
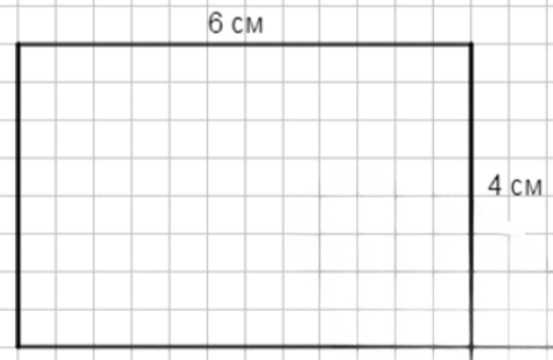
в) Постройте прямоугольник, у которого ширина относится к длине как \(2:3\): например, \(4\text{ см}\) и \(6\text{ см}\). Отношение сторон \(4:6=2:3\).
а) Требуется начертить прямоугольник, у которого отношение длины к ширине равно \(2:1\). Это значит, что одна сторона должна быть в два раза больше другой: если обозначить ширину через \(x\), то длина равна \(2x\). Для наглядной и удобной отрисовки выбираем удобные целые сантиметры, чтобы сохранить точные пропорции на клетчатой бумаге. Возьмем ширину \(3\text{ см}\), тогда длина должна быть \(2\cdot 3=6\text{ см}\). Проверим: отношение \(6:3\) сокращаем на \(3\), получаем \(2:1\), что полностью удовлетворяет условию. При построении на клетках откладываем по горизонтали \(6\text{ см}\), по вертикали \(3\text{ см}\), соединяем точки параллельными прямыми; получаем требуемый прямоугольник с корректно выдержанными пропорциями.
б) Здесь нужно отношение сторон \(1:1\), то есть обе стороны равны. Пусть каждая сторона равна \(3\text{ см}\). Тогда получаем фигуру, у которой все углы прямые и противоположные стороны попарно равны, а дополнительно смежные стороны тоже равны. Это частный случай прямоугольника, поэтому такая фигура называется квадрат. Проверка пропорций: отношение \(3:3=1:1\). При построении удобно отложить по горизонтали и вертикали по \(3\text{ см}\) от одной вершины, затем провести параллели и замкнуть контур; диагонали будут равны и взаимно перпендикулярны, что соответствует свойствам квадрата как прямоугольника с равными сторонами.
в) Необходимо отношение сторон \(2:3\). Это означает, что меньшая сторона составляет \(\frac{2}{3}\) от большей. Выберем размеры, кратные числам \(2\) и \(3\), чтобы соблюсти масштаб без дробных значений. Возьмем меньшую сторону \(4\text{ см}\) и большую \(6\text{ см}\). Проверка: отношение \(4:6\) сокращаем на \(2\), получаем \(2:3\), что верно. Для построения на клетках отложим по горизонтали \(6\text{ см}\) и по вертикали \(4\text{ см}\), затем проведем параллельные стороны и замкнем прямоугольник. При желании можно масштабировать эти размеры, умножая обе стороны на одно и то же число \(k>0\), так как если исходно стороны \(2\) и \(3\), то при масштабировании до \(2k\) и \(3k\) отношение остаётся \(2:3\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!