
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.52 Виленкин, Жохов — Подробные Ответы
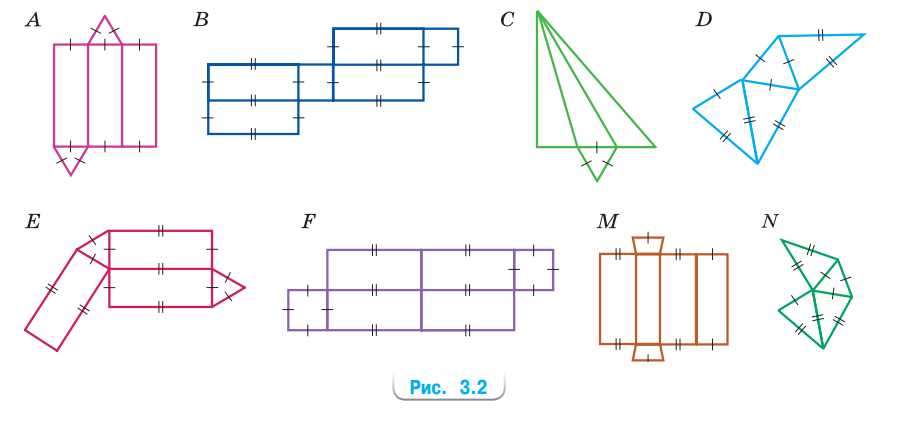
Какие фигуры (рис. 3.2) являются развёртками (штрихами отмечены равные отрезки):
а) треугольной призмы; б) четырёхугольной призмы; в) треугольной пирамиды?
а) Разверткой треугольной призмы является фигура \( A \), так как призма с треугольным основанием разворачивается в две треугольные грани и три прямоугольных боковых грани, что соответствует фигуре \( A \).
б) Разверткой четырёхугольной призмы является фигура \( B \), так как призма с четырёхугольным основанием разворачивается в две четырёхугольные грани и четыре прямоугольных боковых грани, что соответствует фигуре \( B \).
в) Разверткой треугольной пирамиды является фигура \( D \), поскольку пирамида с треугольным основанием разворачивается в одну треугольную грань основания и три треугольных боковых грани, что соответствует фигуре \( D \).
а) Треугольная призма состоит из двух треугольных оснований и трёх прямоугольных боковых граней. При развёртывании такой призмы все её грани раскладываются в одну плоскость, образуя фигуру, состоящую из двух треугольников и трёх прямоугольников, соединённых друг с другом. Эта фигура соответствует фигуре \( A \), так как именно она включает все необходимые грани призмы. Важно понимать, что боковые грани призмы всегда являются прямоугольниками, а основания — треугольниками, что и отражено в фигуре \( A \).
б) Четырёхугольная призма имеет два четырёхугольных основания и четыре боковые грани, которые являются прямоугольниками. При развёртывании призмы все эти грани располагаются в одной плоскости, образуя фигуру, состоящую из двух четырёхугольников и четырёх прямоугольников, соединённых по сторонам. Фигура \( B \) именно такова, что подтверждает её соответствие развёртке четырёхугольной призмы. Таким образом, можно видеть, что количество боковых граней равно количеству сторон основания, и все они развёрнуты в плоскость.
в) Треугольная пирамида состоит из одного треугольного основания и трёх треугольных боковых граней, которые сходятся в вершине. При развёртывании пирамиды все её грани раскрываются в плоскость, образуя фигуру из четырёх треугольников: одного основания и трёх боковых граней. Эта фигура соответствует фигуре \( D \), так как она включает все необходимые треугольные грани. Важный момент — боковые грани пирамиды всегда треугольные, а их количество равно количеству сторон основания, что и отражено в фигуре \( D \).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!