ГДЗ по Математике 6 Класс Часть 1 Номер 3.188 Виленкин, Жохов — Подробные Ответы

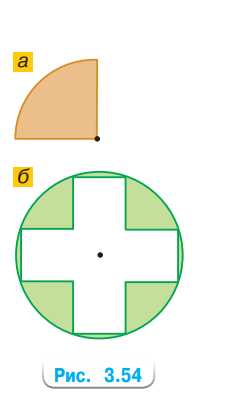
Выполните измерения и вычислите площадь каждой закрашенной фигуры (рис. 3.54).

1) Радиус четверти круга равен 1,5 см.
Площадь фигуры равна:
\( S = \frac{\pi r^2}{4} = \frac{3{,}14 \cdot 1{,}5^2}{4} = \frac{3{,}14 \cdot 2{,}25}{4} = \frac{7{,}065}{4} = 1{,}76625 \, (\text{см}^2) \approx 1{,}8 \, (\text{см}^2) \).

2) Крест состоит из пяти одинаковых квадратов со стороной 1 см.
Площадь креста равна \( 5 \cdot 1 = 5 \, \text{см}^2 \).
Радиус круга равен 1,5 см.
Площадь круга равна:
\( S = \pi r^2 = 3{,}14 \cdot 1{,}5^2 = 3{,}14 \cdot 2{,}25 = 7{,}065 \, (\text{см}^2) \).
Площадь закрашенной фигуры равна:
\( 7{,}065 — 5 = 2{,}065 \, (\text{см}^2) \approx 2{,}1 \, (\text{см}^2) \).

1) Радиус четверти круга равен 1,5 см. Для нахождения площади четверти круга нужно сначала найти площадь полного круга, а затем разделить её на 4, так как четверть круга — это одна из четырёх равных частей полного круга. Полная площадь круга вычисляется по формуле \( S = \pi r^2 \), где \( r \) — радиус круга. Подставляем значение радиуса: \( r = 1{,}5 \) см, тогда площадь круга будет равна \( 3{,}14 \cdot 1{,}5^2 \).

Вычислим \( 1{,}5^2 \), что равно \( 2{,}25 \). Далее умножаем число \( \pi \approx 3{,}14 \) на \( 2{,}25 \), получаем \( 7{,}065 \). Чтобы найти площадь четверти круга, делим это число на 4:
\( S = \frac{7{,}065}{4} = 1{,}76625 \, \text{см}^2 \). Округляем до десятых и получаем \( 1{,}8 \, \text{см}^2 \). Таким образом, площадь четверти круга с радиусом 1,5 см равна примерно \( 1{,}8 \, \text{см}^2 \).

2) Крест состоит из пяти одинаковых квадратов со стороной 1 см. Чтобы найти площадь креста, нужно сложить площади всех пяти квадратов. Площадь одного квадрата равна \( 1 \cdot 1 = 1 \, \text{см}^2 \), так как сторона квадрата равна 1 см. Значит площадь пяти квадратов равна \( 5 \cdot 1 = 5 \, \text{см}^2 \).

Радиус круга, в который вписан крест, равен 1,5 см. Площадь полного круга с этим радиусом вычисляется по формуле \( S = \pi r^2 = 3{,}14 \cdot 1{,}5^2 = 3{,}14 \cdot 2{,}25 = 7{,}065 \, \text{см}^2 \). Чтобы найти площадь закрашенной фигуры, нужно из площади круга вычесть площадь креста, так как крест внутри круга не закрашен. Вычитаем:
\( 7{,}065 — 5 = 2{,}065 \, \text{см}^2 \). Округляем до десятых и получаем \( 2{,}1 \, \text{см}^2 \).

Таким образом, площадь закрашенной части фигуры, которая получается при вычитании площади креста из площади круга, равна примерно \( 2{,}1 \, \text{см}^2 \).