ГДЗ по Математике 6 Класс Часть 1 Номер 3.172 Виленкин, Жохов — Подробные Ответы

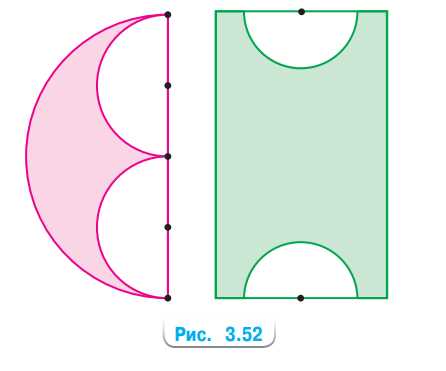
Сделайте необходимые измерения и вычислите площади закрашенных фигур, изображённых на рисунке 3.52.

1) Радиус меньших половинок круга \(r_1 = 1{,}2\) см, радиус большего полукруга \(r_2 = 2{,}5\) см.
Площадь закрашенной фигуры найдём как разность площади большого полукруга и площади двух меньших половинок:
\(S = \frac{\pi r_2^2}{2} — 2 \cdot \frac{\pi r_1^2}{2} = \frac{\pi r_2^2}{2} — \pi r_1^2 = 3{,}14 \cdot \frac{2{,}5^2}{2}-\)
\( — 3{,}14 \cdot 1{,}2^2 = 3{,}14 \cdot 3{,}125 — 3{,}14 \cdot 1{,}44 = 9{,}8125 — 4{,}5216 = 5{,}2909 \text{ см}^2.\)

2) Радиус полукругов \(r = 1\) см, размеры прямоугольника \(3 \times 5\) см.
Площадь закрашенной фигуры равна площади прямоугольника минус площадь круга:
\(S = ab — \pi r^2 = 3 \cdot 5 — 3{,}14 \cdot 1^2 = 15 — 3{,}14 = 11{,}86 \text{ см}^2.\)

1) Для первой фигуры нам даны радиусы двух половинок круга: меньших половинок с радиусом \(r_1 = 1{,}2\) см и большего полукруга с радиусом \(r_2 = 2{,}5\) см. Чтобы найти площадь закрашенной фигуры, нужно сначала понять, что она состоит из большого полукруга, из которого вычитаются две меньшие половинки круга. Площадь полукруга вычисляется как половина площади круга, то есть \( \frac{\pi r^2}{2} \), где \(r\) — радиус. Значит, площадь большого полукруга равна \( \frac{\pi r_2^2}{2} \), а площадь каждой меньшей половинки равна \( \frac{\pi r_1^2}{2} \).

Далее, поскольку вычитаются две меньшие половинки, суммарная площадь вычитаемых фигур будет равна \( 2 \cdot \frac{\pi r_1^2}{2} = \pi r_1^2 \). Таким образом, площадь закрашенной фигуры находится по формуле
\( S = \frac{\pi r_2^2}{2} — \pi r_1^2 \). Подставим численные значения:
\( S = 3{,}14 \cdot \frac{2{,}5^2}{2} — 3{,}14 \cdot 1{,}2^2 = 3{,}14 \cdot \frac{6{,}25}{2} — 3{,}14 \cdot 1{,}44 =\)
\(= 3{,}14 \cdot 3{,}125 — 3{,}14 \cdot 1{,}44 \).

Выполним умножения: \( 3{,}14 \cdot 3{,}125 = 9{,}8125 \), \( 3{,}14 \cdot 1{,}44 = 4{,}5216 \). После этого вычитаем:
\( 9{,}8125 — 4{,}5216 = 5{,}2909 \text{ см}^2 \). Это и есть площадь закрашенной фигуры в первом случае.

2) Во втором случае радиус полукругов равен \( r = 1 \) см, а размеры прямоугольника — 3 см и 5 см. Закрашенная фигура получается из прямоугольника, из которого вычитаются две половинки круга. Две половинки круга вместе составляют целый круг, поэтому площадь вычитаемой части равна площади круга с радиусом \(r\), то есть \( \pi r^2 \).

Площадь прямоугольника вычисляется как произведение его сторон: \( ab = 3 \cdot 5 = 15 \text{ см}^2 \). Площадь круга равна \( \pi r^2 = 3{,}14 \cdot 1^2 = 3{,}14 \text{ см}^2 \). Следовательно, площадь закрашенной фигуры равна разности:
\( S = ab — \pi r^2 = 15 — 3{,}14 = 11{,}86 \text{ см}^2 \).

Таким образом, во втором случае мы просто вычитаем площадь круга из площади прямоугольника, получая площадь оставшейся закрашенной фигуры. Это решение удобно тем, что не нужно отдельно вычислять половинки круга, а можно использовать площадь полного круга, так как две половинки вместе дают круг.