ГДЗ по Математике 6 Класс Часть 1 Номер 3.168 Виленкин, Жохов — Подробные Ответы

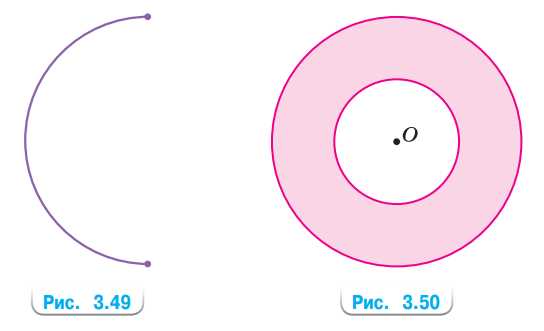
а) На рисунке 3.49 изображена половина окружности. Сделайте необходимые измерения и найдите длину полуокружности.

б) Измерьте радиус каждой окружности и вычислите площадь кольца (рис. 3.50).

а) Диаметр – отрезок, проходящий через центр окружности и соединяющий две точки окружности.
Длина окружности \(C = \pi d\), где \(\pi = 3{,}14\).
Длина полуокружности равна половине длины окружности:
\(C_{\text{полу}} = \frac{\pi d}{2}\).
Измерили диаметр \(d = 4{,}4 \text{ см}\).
Тогда
\(C_{\text{полу}} = \frac{3{,}14 \cdot 4{,}4}{2} = \frac{13{,}816}{2} = 6{,}908 \text{ см}\).

Ответ: \(6{,}908 \text{ см}\).

б) Радиус – отрезок, соединяющий центр с точкой окружности.
Площадь круга \(S = \pi r^2\).
Для заштрихованной фигуры нужно найти разность площадей большого и малого кругов:
\(S_2 — S_1\).
Измерили радиусы: \(r = 1{,}1 \text{ см}\), \(R = 2{,}2 \text{ см}\).
Площади:
\(S_1 = 3{,}14 \cdot 1{,}1^2 = 3{,}14 \cdot 1{,}21 = 3{,}7994 \text{ см}^2\),
\(S_2 = 3{,}14 \cdot 2{,}2^2 = 3{,}14 \cdot 4{,}84 = 15{,}1976 \text{ см}^2\).
Разность:
\(S_2 — S_1 = 15{,}1976 — 3{,}7994 = 11{,}3982 \text{ см}^2\).

Ответ: \(11{,}3982 \text{ см}^2\).

а) Диаметр окружности — это отрезок, который проходит через центр окружности и соединяет две точки на её границе. Этот отрезок является самой длинной хордой в окружности. Длина окружности вычисляется по формуле \(C = \pi d\), где \(d\) — диаметр, а \(\pi\) — математическая константа, приблизительно равная 3,14. Для вычисления длины полуокружности достаточно взять половину длины всей окружности, так как полуокружность — это ровно половина окружности.

Для измерения диаметра необходимо приложить линейку так, чтобы её нулевое деление совпало с одной из крайних точек окружности, а сама линейка проходила через центр и другую крайнюю точку. Измеренное значение диаметра равно \(d = 4{,}4 \text{ см}\). Подставляя это значение в формулу длины полуокружности, получаем:
\(C_{\text{полу}} = \frac{\pi d}{2} = \frac{3{,}14 \cdot 4{,}4}{2}\).

Произведя вычисления, сначала умножаем \(\pi\) на диаметр: \(3{,}14 \cdot 4{,}4 = 13{,}816\). Затем делим результат на 2, так как полуокружность — половина окружности:
\(C_{\text{полу}} = \frac{13{,}816}{2} = 6{,}908 \text{ см}\). Это и есть длина полуокружности, соответствующая диаметру 4,4 см.

б) Радиус — это отрезок, соединяющий центр окружности с любой точкой на её границе. Он всегда равен половине диаметра. Площадь круга вычисляется по формуле \(S = \pi r^2\), где \(r\) — радиус круга. Чтобы найти площадь заштрихованной фигуры, которая представляет собой кольцо, нужно вычислить разность площадей двух кругов с разными радиусами.

Для этого измеряем радиусы меньшего и большего кругов. Линейку располагаем так, чтобы её нулевое деление совпало с центром окружностей, тогда деления на линейке, где проходят окружности, покажут радиусы. Измерения дают: \(r = 1{,}1 \text{ см}\) для меньшего круга и \(R = 2{,}2 \text{ см}\) для большего.

Вычисляем площади каждого круга:
\(S_1 = \pi r^2 = 3{,}14 \cdot 1{,}1^2 = 3{,}14 \cdot 1{,}21 = 3{,}7994 \text{ см}^2\),
\(S_2 = \pi R^2 = 3{,}14 \cdot 2{,}2^2 = 3{,}14 \cdot 4{,}84 = 15{,}1976 \text{ см}^2\).

Площадь заштрихованной фигуры равна разности площадей большого и малого кругов:
\(S_{\text{заштрих}} = S_2 — S_1 = 15{,}1976 — 3{,}7994 = 11{,}3982 \text{ см}^2\). Это и есть искомая площадь кольца, ограниченного двумя окружностями с радиусами 2,2 см и 1,1 см.