ГДЗ по Математике 6 Класс Часть 1 Номер 3.157 Виленкин, Жохов — Подробные Ответы

Начертите треугольник MNT. Постройте треугольник, симметричный треугольнику MNT: а) относительно прямой MN; б) относительно вершины N.

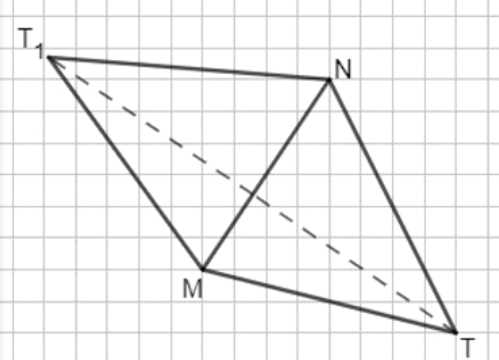
а) Треугольник \( MNT_1 \) получается симметрией треугольника \( MNT \) относительно стороны \( MN \). Это значит, что точка \( T_1 \) — образ точки \( T \) при отражении относительно отрезка \( MN \). Отражение сохраняет длины и углы, следовательно, \( MNT_1 \) и \( MNT \) равны по форме и размеру, но расположены зеркально относительно \( MN \).

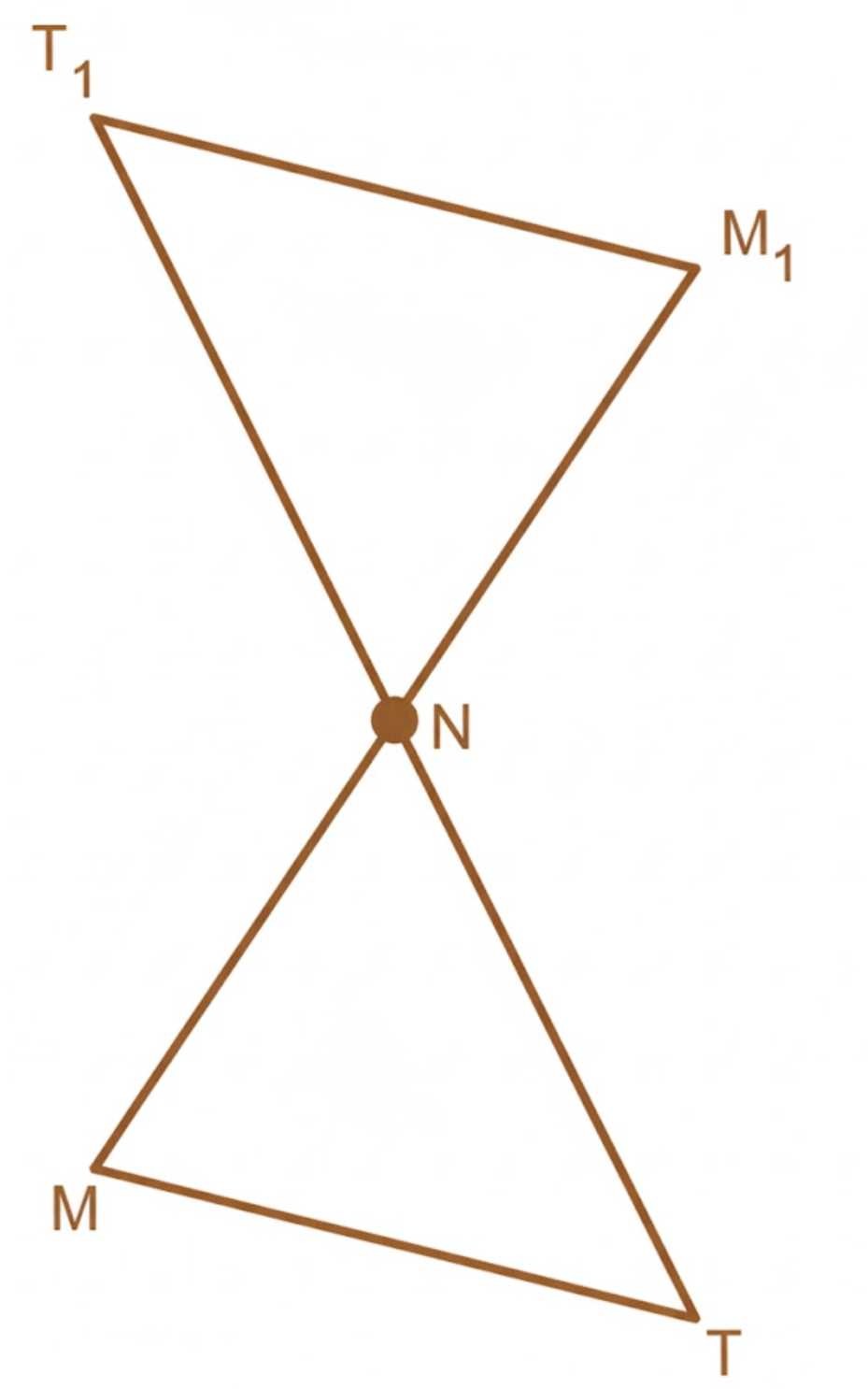
б) Треугольник \( MNT_1 \) симметричен треугольнику \( MNT \) относительно стороны \( NT \). Здесь отражение происходит относительно стороны \( NT \), поэтому точка \( M_1 \) — образ точки \( M \) при отражении относительно \( NT \). Аналогично, треугольники равны по форме и размеру, но расположены зеркально относительно \( NT \).

а) Треугольник \( MNT_1 \) является симметричным треугольнику \( MNT \) относительно стороны \( MN \). Это означает, что при отражении каждой точки треугольника \( MNT \) относительно прямой, содержащей отрезок \( MN \), получается треугольник \( MNT_1 \). При этом точки \( M \) и \( N \) лежат на линии симметрии и остаются неподвижными, а точка \( T \) переходит в точку \( T_1 \). Отражение — это движение, сохраняющее длины отрезков и углы между ними, поэтому треугольники \( MNT \) и \( MNT_1 \) равны по длинам сторон и величинам углов, но расположены зеркально относительно \( MN \).

Отражение относительно стороны \( MN \) можно рассматривать как построение перпендикуляра из точки \( T \) на прямую \( MN \), после чего точка \( T_1 \) располагается на том же расстоянии от \( MN \), но с противоположной стороны. Таким образом, длина перпендикуляра \( TT_1 \) равна удвоенному расстоянию от точки \( T \) до прямой \( MN \). Это свойство отражения обеспечивает, что стороны \( MT \) и \( MT_1 \), а также \( NT \) и \( NT_1 \), имеют одинаковую длину, что подтверждает равенство треугольников.

В итоге, треугольник \( MNT_1 \) является точным зеркальным отражением треугольника \( MNT \) относительно стороны \( MN \). Это значит, что все геометрические свойства исходного треугольника сохраняются, но ориентация меняется на противоположную, что хорошо видно на рисунке, где \( T_1 \) находится с другой стороны от \( MN \) по сравнению с точкой \( T \).

б) В случае, когда треугольник \( MNT_1 \) симметричен треугольнику \( MNT \) относительно стороны \( NT \), отражение происходит относительно прямой, содержащей отрезок \( NT \). При этом точки \( N \) и \( T \) остаются неподвижными, а точка \( M \) переходит в точку \( M_1 \), являющуюся зеркальным образом точки \( M \) относительно линии \( NT \). Отражение сохраняет длины и углы, поэтому треугольники \( MNT \) и \( MNT_1 \) равны по форме и размеру, но расположены зеркально.

Для построения точки \( M_1 \) из точки \( M \) проводят перпендикуляр из \( M \) на прямую \( NT \), после чего откладывают отрезок \( MM_1 \), равный удвоенному расстоянию от \( M \) до линии \( NT \), но в противоположную сторону. Таким образом, точка \( M_1 \) находится на таком же расстоянии от \( NT \), как и \( M \), но с другой стороны. Это обеспечивает равенство отрезков \( NM \) и \( NM_1 \), а также \( TM \) и \( TM_1 \), что подтверждает равенство треугольников.

В результате треугольник \( MNT_1 \) является зеркальным отражением треугольника \( MNT \) относительно стороны \( NT \). При этом все углы и длины соответствующих сторон совпадают, но ориентация треугольника изменена на противоположную. На рисунке видно, что точка \( M_1 \) находится с другой стороны от линии \( NT \) по сравнению с точкой \( M \), что наглядно иллюстрирует действие отражения.