ГДЗ по Математике 6 Класс Часть 1 Номер 3.156 Виленкин, Жохов — Подробные Ответы

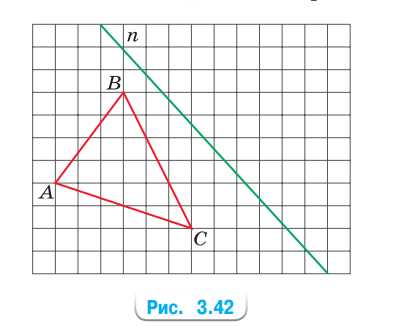
Изобразите рисунок 3.42 в тетради. Постройте треугольник, симметричный треугольнику ABC: а) относительно прямой n; б) относительно вершины A.

а) Треугольник \(A_1 B_1 C_1\) получается отражением треугольника \(ABC\) относительно прямой \(n\). Для каждого угла и стороны треугольника \(ABC\) найдём симметричные точки и отрезки относительно \(n\). Полученный треугольник и будет \(A_1 B_1 C_1\).

б) Треугольник \(AB_1 C_1\) симметричен треугольнику \(ABC\) относительно вершины \(A\). Это значит, что точки \(B_1\) и \(C_1\) — это образы точек \(B\) и \(C\) при центральной симметрии с центром в точке \(A\). То есть для каждой точки, например, \(B\), выполняется равенство векторов: \(\overrightarrow{A B_1} = -\overrightarrow{A B}\), аналогично для \(C_1\).

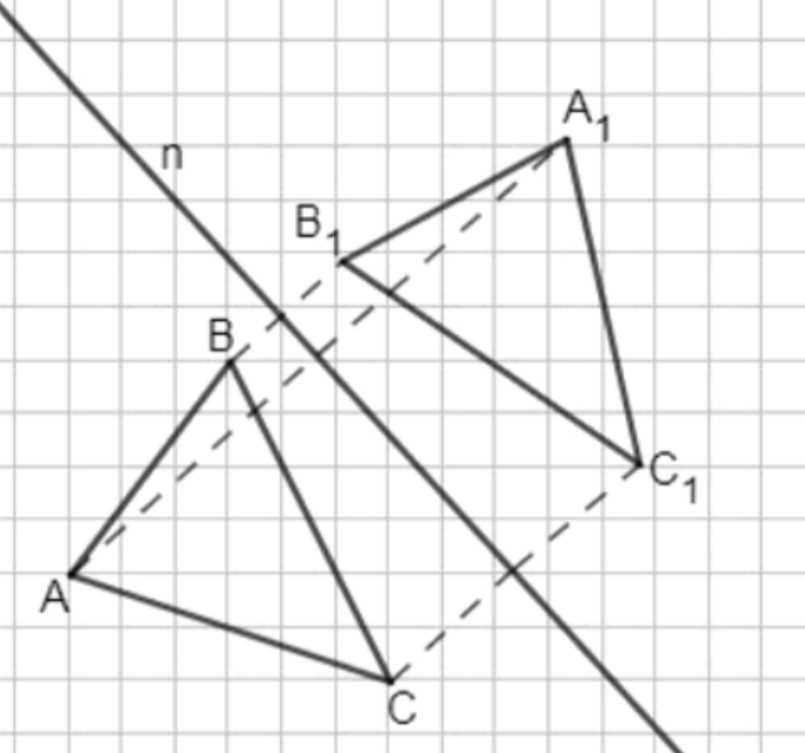
а) Треугольник \(A_1 B_1 C_1\) является симметричным треугольнику \(ABC\) относительно прямой \(n\). Это значит, что каждая точка треугольника \(ABC\) отражается относительно прямой \(n\), и её образом становится соответствующая точка треугольника \(A_1 B_1 C_1\). Отражение относительно прямой — это такая геометрическая операция, при которой прямая \(n\) является осью симметрии: для любой точки \(P\) её образ \(P_1\) лежит на перпендикуляре к прямой \(n\), проходящем через \(P\), и расстояния от \(P\) и \(P_1\) до \(n\) равны. Таким образом, \(A_1\) — это отражение точки \(A\), \(B_1\) — отражение точки \(B\), \(C_1\) — отражение точки \(C\).

В результате отражения сохраняются длины отрезков и углы, то есть треугольник \(A_1 B_1 C_1\) равен треугольнику \(ABC\) по форме и размеру, но расположен зеркально относительно линии \(n\). Это можно проверить, построив перпендикуляры из точек \(A, B, C\) на прямую \(n\) и отложив равные отрезки по другую сторону \(n\). Например, если расстояние от \(B\) до \(n\) равно \(d\), то точка \(B_1\) будет находиться на перпендикуляре к \(n\) на расстоянии \(d\) с другой стороны.

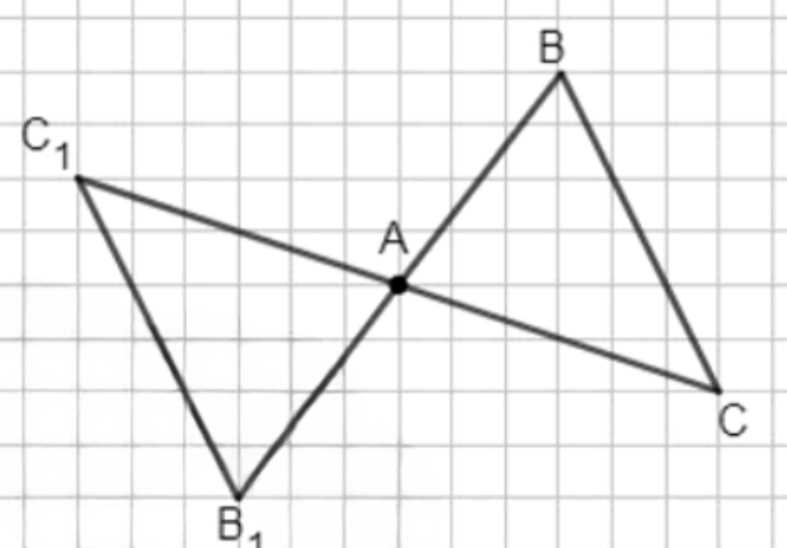
б) Треугольник \(AB_1 C_1\) симметричен треугольнику \(ABC\) относительно вершины \(A\). Центральная симметрия с центром в точке \(A\) означает, что каждая точка \(P\) треугольника \(ABC\) отображается в точку \(P_1\), такую что точка \(A\) является серединой отрезка \(P P_1\). Иными словами, вектор \(\overrightarrow{A P_1}\) равен по величине и противоположен по направлению вектору \(\overrightarrow{A P}\), то есть \(\overrightarrow{A P_1} = — \overrightarrow{A P}\).

Применительно к треугольнику \(ABC\), точки \(B_1\) и \(C_1\) находятся так, что \(A\) — середина отрезков \(B B_1\) и \(C C_1\). Это означает, что координаты точек \(B_1\) и \(C_1\) можно найти, используя формулы \(B_1 = 2A — B\) и \(C_1 = 2A — C\), где сложение и вычитание векторов происходит покоординатно. В результате треугольник \(AB_1 C_1\) является поворотом треугольника \(ABC\) на 180 градусов вокруг точки \(A\), что сохраняет длины и углы, но меняет расположение точек зеркально относительно \(A\).