
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.151 Виленкин, Жохов — Подробные Ответы
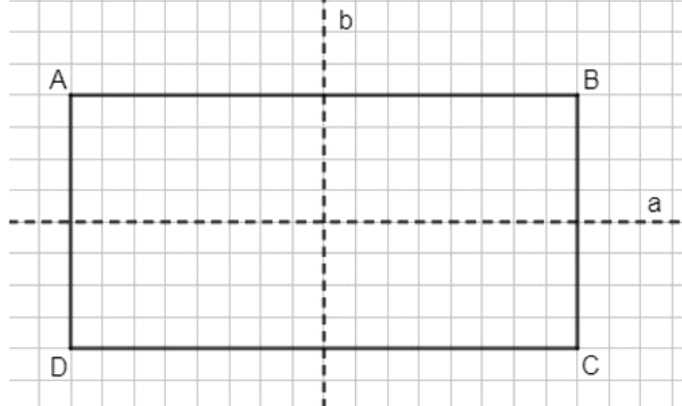
Начертите прямоугольник ABCD и постройте с помощью линейки его оси симметрии.
1. Начертите прямоугольник \(ABCD\).
2. Проведите прямую \(a\), проходящую через середины сторон \(AB\) и \(DC\). Эта прямая является осью симметрии, так как делит прямоугольник на две равные части по горизонтали.
3. Проведите прямую \(b\), проходящую через середины сторон \(AD\) и \(BC\). Эта прямая является осью симметрии, так как делит прямоугольник на две равные части по вертикали.
Таким образом, прямые \(a\) и \(b\) — оси симметрии прямоугольника \(ABCD\).
1. Прямоугольник \(ABCD\) — это четырехугольник, у которого все углы прямые, то есть равны \(90^\circ\), а противоположные стороны равны и параллельны. Для построения осей симметрии необходимо найти линии, которые делят этот прямоугольник на две равные части, зеркально отражающиеся друг в друге. Такие линии называются осями симметрии. В прямоугольнике оси симметрии всегда проходят через середины противоположных сторон.
2. Первая ось симметрии — прямая \(a\). Она проведена горизонтально и проходит через середины сторон \(AB\) и \(DC\). Эта прямая делит прямоугольник на две равные части сверху и снизу. При отражении относительно этой линии верхняя часть \(AB\) совпадает с нижней частью \(DC\), а точки \(A\) и \(B\) переходят в точки \(D\) и \(C\) соответственно. Поэтому прямая \(a\) является осью симметрии, так как сохраняет фигуру при отражении.
3. Вторая ось симметрии — прямая \(b\). Она проведена вертикально и проходит через середины сторон \(AD\) и \(BC\). Эта прямая делит прямоугольник на две равные части слева и справа. При отражении относительно этой линии левая часть \(AD\) совпадает с правой частью \(BC\), а точки \(A\) и \(D\) переходят в точки \(B\) и \(C\) соответственно. Таким образом, прямая \(b\) также является осью симметрии прямоугольника. Следовательно, прямые \(a\) и \(b\) — оси симметрии прямоугольника \(ABCD\).






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!