
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.138 Виленкин, Жохов — Подробные Ответы
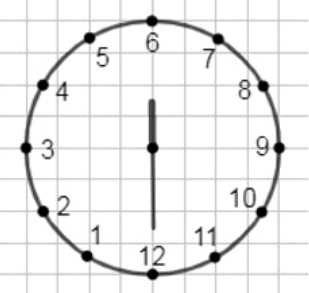
Построили фигуру, симметричную циферблату часов (рис. 3.35) относительно:
а) центра циферблата;
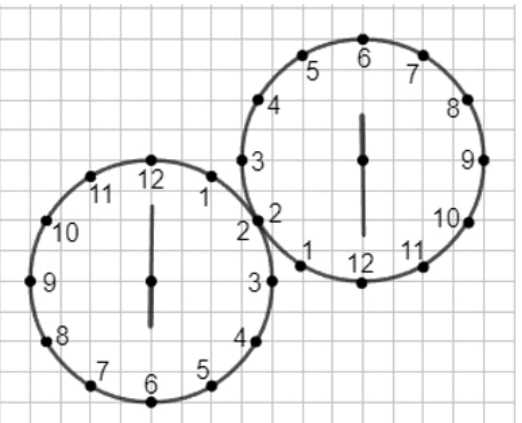
б) некоторой точки, находящейся на окружности циферблата.
Окажется ли симметричный циферблат таким же, как исходный? Подумайте, каково будет направление движения стрелок на симметричных часах в каждом случае.
а) При симметрии относительно центра циферблата часовая стрелка, которая была внизу (6 часов), становится вверху (12 часов), а минутная стрелка, которая была вверху (12 часов), становится внизу (6 часов). Направление движения стрелок не меняется.
б) При симметрии относительно точки на окружности циферблата часовая стрелка также становится вверху, а минутная — внизу, при этом движение стрелок не изменяется.
а) Симметрия относительно центра циферблата означает, что каждая точка на циферблате отражается через центр на точку, расположенную на противоположной стороне окружности. Если часовая стрелка указывает вниз (на 6 часов), то после такой симметрии она окажется вверху (на 12 часов). Аналогично, минутная стрелка, которая была вверху (на 12 часов), после отражения окажется внизу (на 6 часов). При этом направление движения стрелок не изменяется, так как симметрия не меняет порядок следования точек по окружности. Таким образом, движение стрелок сохраняется, только их положение меняется на противоположное относительно центра.
б) Симметрия относительно некоторой точки на окружности циферблата — это отражение через эту точку. При этом каждая точка циферблата отображается в другую точку на той же окружности, но уже сдвинутую относительно исходного положения. Если выбрать точку симметрии на окружности, например, в позиции между 1 и 2 часами, то часовая стрелка, указывавшая вниз (на 6 часов), после отражения окажется вверху (на 12 часов), а минутная стрелка, которая была вверху (на 12 часов), станет внизу (на 6 часов). Это происходит потому, что отражение относительно точки на окружности сохраняет расположение стрелок на окружности, но меняет их местами по симметрии.
В обоих случаях движение стрелок не изменяется, так как симметрии не меняют направление обхода циферблата. Если обозначить угол поворота стрелки как \(\theta\), то после симметрии угол изменится на \(\theta’ = \theta + \pi\) (при отражении через центр) или на соответствующий угол в случае отражения через точку на окружности, но направление вращения останется прежним. Следовательно, симметрия меняет только положение стрелок, а не их движение.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.






Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!