
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.136 Виленкин, Жохов — Подробные Ответы
Могут ли пересекаться:
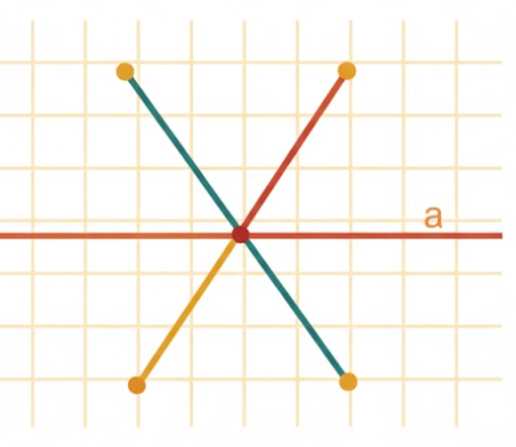
а) два отрезка, симметричные относительно прямой; б) два центрально-симметричных отрезка? Ответы проиллюстрируйте рисунком.
а) Два отрезка, симметричных относительно прямой, могут пересекаться в точке пересечения с этой прямой.
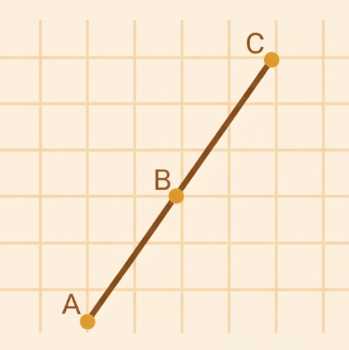
б) Два центрально-симметричных отрезка не могут пересекаться, они могут иметь только общую точку — центр симметрии. Например, отрезок \(AB\) симметричен отрезку \(BC\) относительно точки \(B\).
а) Два отрезка, симметричных относительно прямой, могут пересекаться в точке, которая лежит на этой прямой симметрии. Это происходит потому, что при отражении относительно прямой каждая точка отрезка переходит в точку другого отрезка, а точки, лежащие на самой прямой, остаются неподвижными. Если отрезки пересекаются именно на этой прямой, то их симметричное отражение сохраняет эту точку пересечения. Таким образом, пересечение возможно и происходит именно в точке пересечения с осью симметрии.
При этом важно понимать, что если отрезки лежат по разные стороны от прямой симметрии, то они как бы «зеркально» отображаются друг в друга, и точка пересечения на прямой является общей для обоих отрезков. Это значит, что отрезки могут иметь общую точку, и эта точка лежит ровно на линии симметрии, обозначенной буквой \(a\) на рисунке. В других местах, отличных от прямой, пересечения не будет, так как отражение меняет расположение точек относительно прямой.
б) В случае центральной симметрии два отрезка, симметричных относительно точки, не могут пересекаться, за исключением случая, когда они имеют общую точку — центр симметрии. Центральная симметрия означает, что каждая точка одного отрезка отображается в точку другого отрезка так, что центр симметрии является серединой отрезка, соединяющего эти точки. Если отрезки пересекались бы в какой-то другой точке, не совпадающей с центром симметрии, это нарушало бы условие симметрии.
На рисунке показано, что отрезок \(AB\) симметричен отрезку \(BC\) относительно точки \(B\). Точка \(B\) является центром симметрии, и именно в ней отрезки могут иметь общую точку. В остальных случаях отрезки не пересекаются, так как центральная симметрия сохраняет направление и длину, но меняет расположение относительно центра, не допуская пересечений вне центра.
Таким образом, при центральной симметрии пересечение двух отрезков возможно только в точке симметрии, а при симметрии относительно прямой пересечение возможно на самой прямой симметрии. Это ключевое различие между двумя видами симметрии, отражённое на рисунках.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!