ГДЗ по Математике 6 Класс Часть 1 Номер 3.135 Виленкин, Жохов — Подробные Ответы

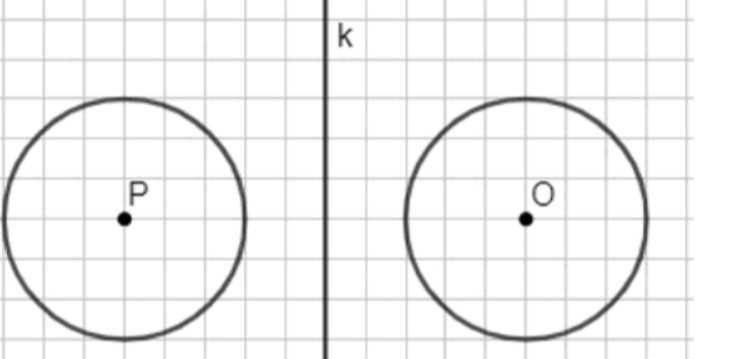
а) Начертите окружность с центром P и прямую k, не пересекающую эту окружность. Постройте окружность с центром O, симметричную этой окружности относительно оси k.

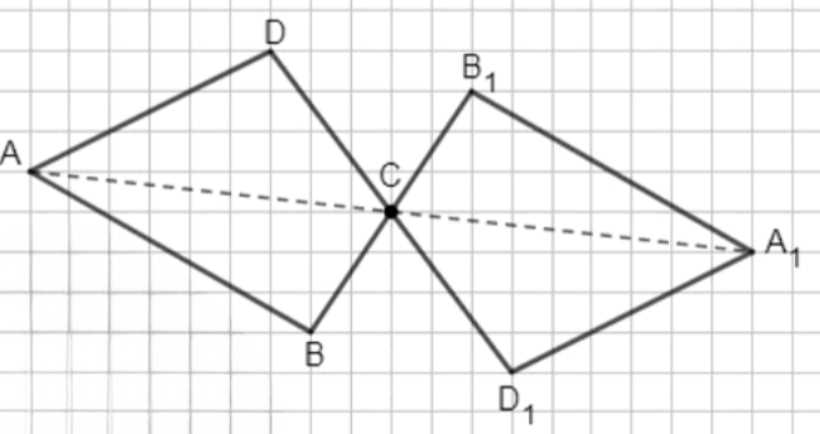
б) Постройте фигуру симметричную относительно точки C для четырёхугольника ABCD на рисунке 3.31.

а) Окружность \(O\) симметрична окружности \(P\) относительно прямой \(k\), если центры окружностей \(O\) и \(P\) симметричны относительно прямой \(k\), а радиусы равны.

б) Четырехугольник \(A_1 B_1 C D_1\) симметричен четырехугольнику \(ABCD\) относительно точки \(C\), если для каждой вершины исходного четырехугольника точка симметрии является серединой отрезка, соединяющего соответствующие вершины:
\(C\) — середина отрезков \(AA_1\), \(BB_1\), \(DD_1\).
То есть для каждой пары вершин выполняется
\(C = \frac{A + A_1}{2}\), \(C = \frac{B + B_1}{2}\), \(C = \frac{D + D_1}{2}\).

а) Окружности \(O\) и \(P\) симметричны относительно прямой \(k\), если при отражении каждой точки окружности \(P\) относительно \(k\) получается соответствующая точка окружности \(O\). Это возможно только в том случае, если центры окружностей \(O\) и \(P\) симметричны относительно прямой \(k\), а радиусы окружностей равны. Центр окружности \(P\) располагается на некотором расстоянии от прямой \(k\), и при отражении через \(k\) он переходит в центр окружности \(O\), который находится на таком же расстоянии, но с другой стороны от \(k\). При этом радиус не меняется, так как отражение сохраняет расстояния.

Таким образом, условие симметрии окружностей сводится к равенству радиусов и симметричному расположению центров относительно прямой \(k\). Если обозначить центр окружности \(P\) как \(P(x_1, y_1)\), центр окружности \(O\) как \(O(x_2, y_2)\), а прямая \(k\) — как ось симметрии, то отражение точки \(P\) относительно \(k\) даёт точку \(O\). Это значит, что \(k\) является серединным перпендикуляром к отрезку \(PO\).

б) Четырехугольник \(A_1 B_1 C D_1\) симметричен четырехугольнику \(ABCD\) относительно точки \(C\), если для каждой вершины исходного четырехугольника существует соответствующая вершина в симметричном четырехугольнике, такая что точка \(C\) является серединой отрезка, соединяющего эти вершины. То есть точка \(C\) — центр симметрии, и выполняется условие \(C = \frac{A + A_1}{2}\), \(C = \frac{B + B_1}{2}\), \(C = \frac{D + D_1}{2}\).

Это означает, что при симметрии относительно точки \(C\) каждая точка \(X\) исходного четырехугольника переходит в точку \(X_1\), расположенную так, что \(C\) — середина отрезка \(XX_1\). Геометрически это значит, что вектор от \(C\) к \(X_1\) равен по длине и противоположен по направлению вектору от \(C\) к \(X\), то есть \( \overrightarrow{CX_1} = — \overrightarrow{CX} \).

Таким образом, симметрия четырехугольников относительно точки \(C\) сохраняет форму и размеры, меняя расположение вершин на противоположное относительно точки \(C\). Это преобразование называется центральной симметрией и является движением в геометрии, сохраняющим длины и углы.