ГДЗ по Математике 6 Класс Часть 1 Номер 3.134 Виленкин, Жохов — Подробные Ответы

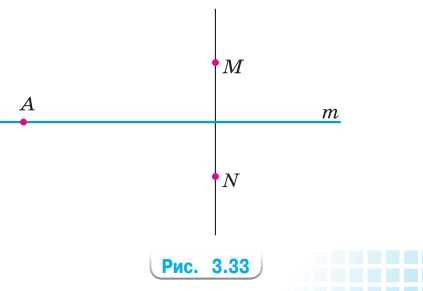
 Убедитесь, используя линейку, что точка A, лежащая на оси симметрии m, одинаково удалена от симметричных относительно прямой m точек M и N (рис. 3.33).

\(AM = AN.\)

Точка \(A\), лежащая на оси симметрии, равноудалена от точек \(M\) и \(N\).

Полученный вывод справедлив для любой точки оси симметрии.

\(AM = AN.\)

Если точка \(A\) лежит на оси симметрии, то она находится на равном расстоянии от двух точек \(M\) и \(N\), которые являются симметричными относительно этой оси. Это означает, что отрезки \(AM\) и \(AN\) равны по длине, так как ось симметрии делит пространство так, что каждая точка с одной стороны оси имеет зеркальное отображение с другой стороны. Следовательно, расстояния от точки \(A\) до \(M\) и до \(N\) совпадают.

Данный факт можно объяснить с помощью геометрии: если провести перпендикуляр от точки \(A\) к оси симметрии, то проекции точек \(M\) и \(N\) на эту ось будут совпадать, а расстояния от \(A\) до этих точек будут равны, так как \(M\) и \(N\) симметричны относительно оси. Таким образом, точка \(A\), лежащая на оси симметрии, является центром равных отрезков \(AM\) и \(AN\).

Этот вывод справедлив для любой точки, расположенной на оси симметрии, независимо от положения точек \(M\) и \(N\). Если изменить положение точки \(A\) вдоль оси, равенство \(AM = AN\) всегда будет сохраняться, что подтверждает фундаментальное свойство оси симметрии — она уравнивает расстояния до пар симметричных точек.