
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.132 Виленкин, Жохов — Подробные Ответы
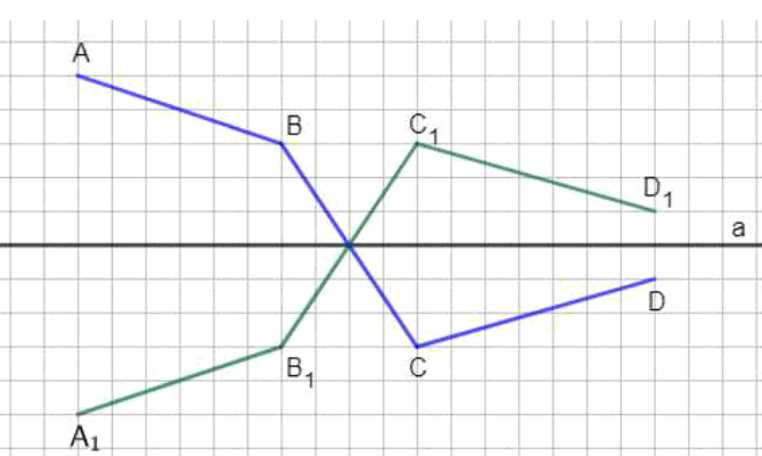
Начертите ломаную из трёх звеньев. Постройте симметричную ей фигуру относительно прямой, проходящей через среднее звено этой ломаной.
1. Пусть дана ломаная \( ABCD \) с тремя звеньями: \( AB \), \( BC \), \( CD \).
2. Найдите среднее звено — отрезок \( BC \).
3. Проведите прямую \( a \) через отрезок \( BC \).
4. Для построения симметричной ломаной \( A_1 B_1 C_1 D_1 \) относительно прямой \( a \) найдите симметричные точки:
— \( B_1 = B \), \( C_1 = C \) (так как они лежат на прямой \( a \)),
— \( A_1 \) — симметрия точки \( A \) относительно \( a \),
— \( D_1 \) — симметрия точки \( D \) относительно \( a \).
5. Соедините точки \( A_1 B_1 C_1 D_1 \) последовательно — получится ломаная, симметричная исходной относительно прямой \( a \).
1. Рассмотрим ломаную \( ABCD \), состоящую из трёх звеньев: \( AB \), \( BC \) и \( CD \). Для построения симметричной ломаной относительно прямой, проходящей через среднее звено, нужно сначала определить это среднее звено. В данном случае среднее звено — это отрезок \( BC \). Прямая \( a \) проводится через точки \( B \) и \( C \), то есть через все точки среднего звена ломаной. Эта прямая служит осью симметрии.
2. Для построения симметричной ломаной \( A_1 B_1 C_1 D_1 \) относительно прямой \( a \) необходимо найти симметричные точки к вершинам исходной ломаной. Поскольку прямая \( a \) проходит через точки \( B \) и \( C \), они сами являются центром симметрии, то есть \( B_1 = B \) и \( C_1 = C \). Остальные точки \( A \) и \( D \) отражаются относительно прямой \( a \). Чтобы найти точку \( A_1 \), симметричную \( A \), нужно провести перпендикуляр из точки \( A \) на прямую \( a \), найти точку пересечения \( M \), а затем отложить отрезок \( M A_1 \) равный \( M A \), но по другую сторону прямой \( a \). Аналогично строится точка \( D_1 \), симметричная \( D \).
3. После нахождения всех симметричных точек \( A_1, B_1, C_1, D_1 \) соединяем их последовательно отрезками \( A_1 B_1 \), \( B_1 C_1 \), \( C_1 D_1 \). Полученная ломаная \( A_1 B_1 C_1 D_1 \) будет симметрична исходной ломаной \( ABCD \) относительно прямой \( a \). Таким образом, каждая точка новой ломаной является зеркальным отражением соответствующей точки исходной ломаной относительно оси симметрии.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!