
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.130 Виленкин, Жохов — Подробные Ответы
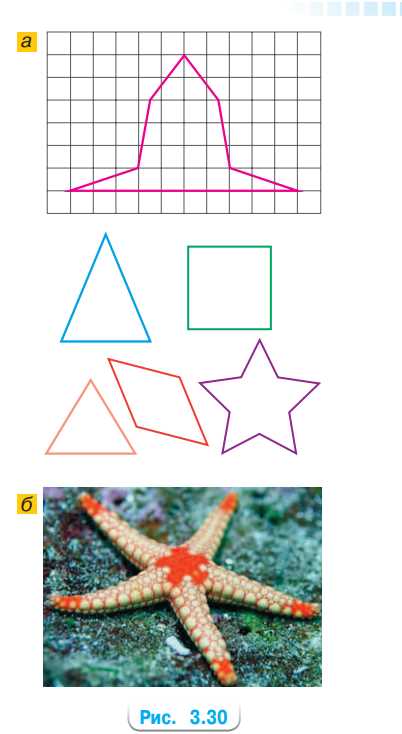
а) На рисунке 3.30, а изображены фигуры. Какие из них имеют одну ось симметрии, две оси симметрии, более двух осей симметрии, имеют центр симметрии?
б) Сколько осей симметрии можно указать на фотографии морской звезды (рис. 3.30, б)? Есть ли у неё центр симметрии?
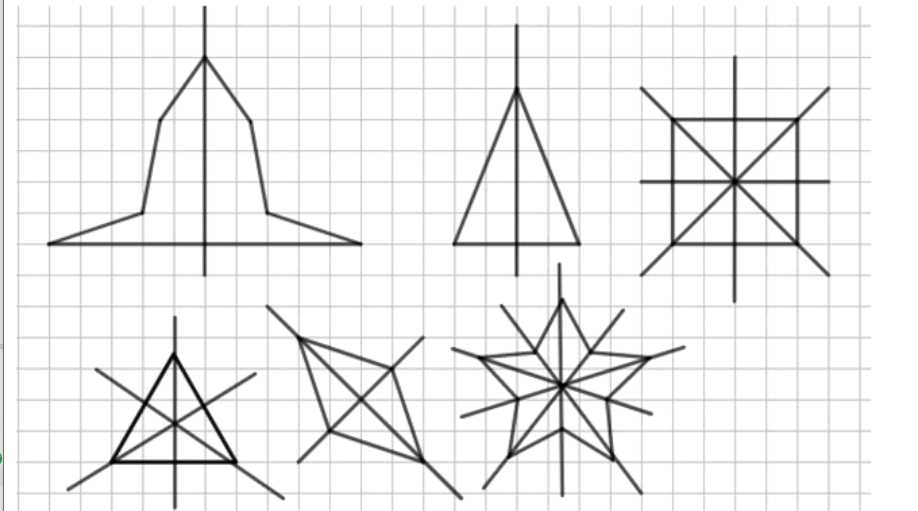
а) Колокольчик и равнобедренный треугольник имеют по одной оси симметрии, так как они симметричны относительно одной линии. Ромб имеет две оси симметрии, проходящие через его вершины и середины сторон. Остальные фигуры имеют более двух осей симметрии.
Центр симметрии есть у ромба и квадрата, так как при повороте на 180° они совпадают сами с собой.
б) Морская звезда имеет пять осей симметрии, которые проходят через её лучи. Центра симметрии у неё нет, так как нельзя повернуть фигуру на 180°, чтобы она совпала сама с собой.
а) Колокольчик и равнобедренный треугольник имеют по одной оси симметрии, потому что у каждой из этих фигур существует одна линия, относительно которой фигура совпадает сама с собой при отражении. Для колокольчика эта ось проходит вертикально через центр, деля фигуру на две зеркально равные части. Аналогично, равнобедренный треугольник симметричен относительно высоты, опущенной на основание, которая является единственной осью симметрии.
Ромб имеет две оси симметрии, которые проходят через его диагонали. Каждая диагональ делит ромб на две равные части, отражение относительно каждой из них сохраняет фигуру. Таким образом, ромб обладает именно двумя осями симметрии, что отличает его от колокольчика и равнобедренного треугольника.
Остальные фигуры на рисунке имеют более двух осей симметрии. Например, квадрат имеет четыре оси симметрии: две проходят через середины противоположных сторон, и две — через диагонали. Центр симметрии есть у ромба и квадрата, так как при повороте на 180° вокруг центра фигура совпадает сама с собой, то есть для точки \(O\) центра симметрии и любой точки \(A\) фигуры существует точка \(A’\), такая что \(O\) — середина отрезка \(AA’\).
б) Морская звезда имеет пять осей симметрии, каждая из которых проходит через один из её пяти лучей и центр фигуры. Отражение относительно любой из этих осей оставляет фигуру неизменной. Однако центра симметрии у морской звезды нет, потому что при повороте на 180° вокруг предполагаемого центра фигура не совпадает сама с собой. Это связано с нечетным числом лучей и их расположением, что не позволяет найти такую точку, вокруг которой фигура была бы центрально симметричной.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!