ГДЗ по Математике 6 Класс Часть 1 Номер 3.129 Виленкин, Жохов — Подробные Ответы

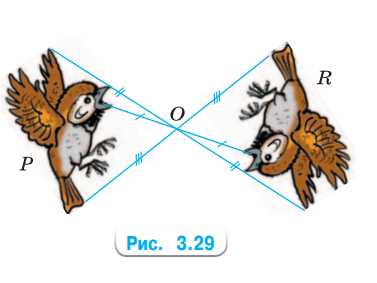
Рассмотрите рисунок 3.29. Как проверить, что фигуры P и R на рисунке симметричны относительно точки O

Фигуры \(P\) и \(R\) центрально-симметричны относительно точки \(O\), потому что их можно совместить, повернув одну из фигур на \(180^\circ\) вокруг центра симметрии.

Фигуры \(P\) и \(R\) называются центрально-симметричными относительно точки \(O\), если существует такая точка \(O\), что при повороте фигуры \(P\) на угол \(180^\circ\) вокруг этой точки она совпадает с фигурой \(R\). Это означает, что для каждой точки \(A\) фигуры \(P\) существует точка \(A’\) фигуры \(R\), расположенная так, что точка \(O\) является серединой отрезка \(AA’\). Таким образом, все точки одной фигуры переходят во все точки другой при данном повороте.

Центр симметрии \(O\) — это точка, вокруг которой можно «перевернуть» фигуру на пол-оборота, то есть на \(180^\circ\), и получить другую фигуру, совпадающую с первой. Если фигуры \(P\) и \(R\) центрально-симметричны относительно \(O\), то поворот на \(180^\circ\) вокруг \(O\) переводит каждую точку \(x\) фигуры \(P\) в точку \(x’\) фигуры \(R\), при этом выполняется соотношение \( \overrightarrow{Ox’} = -\overrightarrow{Ox} \). Это равенство отражает факт, что точки располагаются зеркально относительно центра \(O\).

Следовательно, чтобы проверить центральную симметрию фигур \(P\) и \(R\) относительно точки \(O\), достаточно повернуть одну из фигур на \(180^\circ\) вокруг точки \(O\). Если после такого поворота фигуры совпадут, значит, они центрально-симметричны. Именно поэтому утверждается, что фигуры \(P\) и \(R\) центрально-симметричны относительно точки \(O\), так как их можно совместить поворотом одной из них на угол \(180^\circ\) вокруг центра симметрии \(O\).