
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.128 Виленкин, Жохов — Подробные Ответы
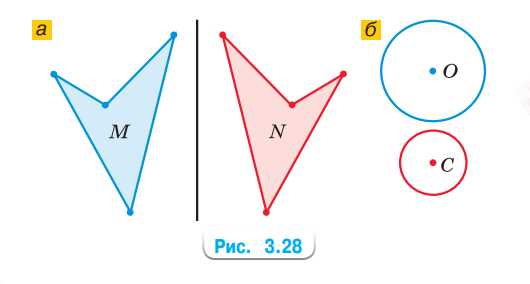
а) Рассмотрите рисунок 3.28, а. Как проверить, что фигуры M и N на рисунке симметричны относительно данной прямой?
б) На рисунке 3.28, б изображены две окружности. Какая прямая служит их общей осью симметрии?
а) Фигуры \( M \) и \( N \) симметричны относительно данной прямой, потому что при перегибании листа бумаги по оси симметрии фигуры \( M \) и \( N \) совпадут.
б) Прямая, проведённая через центры окружностей \( O \) и \( C \), служит их общей осью симметрии.
а) Фигуры \( M \) и \( N \) считаются симметричными относительно данной прямой, потому что эта прямая является осью симметрии. Это значит, что если мысленно или физически перегнуть лист бумаги по этой прямой, то фигура \( M \) совместится с фигурой \( N \). В геометрии ось симметрии — это такая прямая, при отражении относительно которой одна фигура переходит в другую или совпадает сама с собой. Таким образом, наличие оси симметрии гарантирует, что все точки фигуры \( M \) имеют соответствующие точки в фигуре \( N \), расположенные на равном расстоянии от оси, но по разные стороны.
Перегибание листа бумаги — это наглядный способ проверить симметрию. Если при таком действии фигуры совпадают, значит, они действительно симметричны, а прямая, по которой происходит сгибание, является осью симметрии. Это подтверждает, что расстояния от каждой точки фигуры \( M \) до оси равны расстояниям от соответствующих точек фигуры \( N \) до той же оси, но с противоположной стороны. Таким образом, фигуры \( M \) и \( N \) являются зеркальным отражением друг друга относительно этой прямой.
б) Прямая, проведённая через центры окружностей \( O \) и \( C \), служит их общей осью симметрии, потому что центры окружностей лежат на этой прямой, и при отражении относительно неё одна окружность переходит в другую. Ось симметрии для двух окружностей — это прямая, которая делит отрезок, соединяющий их центры, пополам и отражает одну окружность в другую. Поскольку каждая точка окружности находится на фиксированном расстоянии от центра, при отражении относительно этой прямой расстояния сохраняются, и окружности совпадают.
Таким образом, если провести прямую через центры окружностей \( O \) и \( C \), то эта прямая будет осью симметрии, так как отражение относительно неё переводит одну окружность в другую. Это означает, что фигуры окружностей симметричны относительно этой прямой, и она является их общей осью симметрии.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!