ГДЗ по Математике 6 Класс Часть 1 Номер 3.122 Виленкин, Жохов — Подробные Ответы

Начертите план одной из комнат в вашей квартире, доме, измерив её длину и ширину. Выберите масштаб \( \frac{1}{100} \).

а) Пусть длина комнаты на плане равна \( x \) см. Составляем пропорцию:
\( x : 450 = 1 : 100 \)
\( 100x = 450 \)
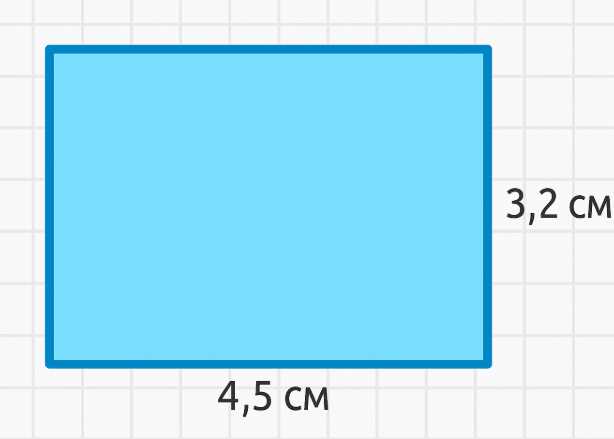
\( x = \frac{450}{100} = 4{,}5 \) см — длина комнаты на плане.

б) Пусть ширина комнаты на плане равна \( y \) см. Составляем пропорцию:
\( y : 320 = 1 : 100 \)
\( 100y = 320 \)
\( y = \frac{320}{100} = 3{,}2 \) см — ширина комнаты на плане.

а) Длина комнаты на плане обозначена через \( x \) сантиметров. Из условия известно, что реальная длина комнаты равна 450 см. На плане используется масштаб 1 : 100, что значит, что 1 см на плане соответствует 100 см в реальности. Чтобы найти длину комнаты на плане, составляем пропорцию: отношение длины на плане к реальной длине равно отношению 1 к 100, то есть \( x : 450 = 1 : 100 \). Это означает, что длина на плане в \( x \) сантиметров соответствует длине в 450 см в реальности, и при этом масштаб равен 1 к 100.

Далее уравнение пропорции можно переписать в виде произведения крест-накрест: \( 100x = 450 \). Для нахождения \( x \) нужно обе части уравнения разделить на 100, получаем \( x = \frac{450}{100} \). Выполнив деление, находим, что \( x = 4{,}5 \) см. Это значит, что длина комнаты на плане составляет 4,5 сантиметра, что соответствует масштабу 1 : 100.

б) Аналогично решается задача для ширины комнаты. Пусть ширина на плане равна \( y \) сантиметров, а реальная ширина комнаты — 320 см. Используем тот же масштаб 1 : 100, значит, \( y : 320 = 1 : 100 \). Это пропорция, в которой ширина на плане относится к реальной ширине, как 1 к 100. Записываем уравнение: \( 100y = 320 \). Для нахождения \( y \) делим обе части на 100, получаем \( y = \frac{320}{100} = 3{,}2 \) см. Таким образом, ширина комнаты на плане равна 3,2 сантиметра.