
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 3.105 Виленкин, Жохов — Подробные Ответы
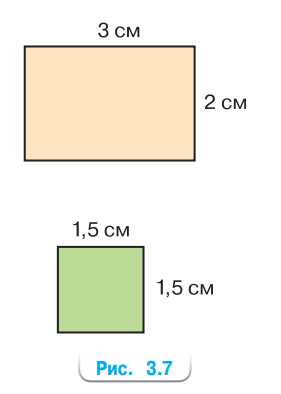
На рисунке 3.7 изображены два участка земли в масштабе 1 : 50 000. Найдите их действительные размеры, периметр и площадь.
1) Пусть размеры участка на местности равны \(x\) см и \(y\) см.
а) Составим пропорцию для длины: \(5,6 : x = 1 : 50000\).
Решаем: \(x = 5,6 \cdot 50000 = 280000\) см.
Переводим в километры: \(280000 \text{ см} = 2800 \text{ м} = 2,8 \text{ км}\) — длина участка.
б) Для ширины: \(2,8 : x = 1 : 50000\).
Решаем: \(x = 2,8 \cdot 50000 = 140000\) см.
Переводим в километры: \(140000 \text{ см} = 1400 \text{ м} = 1,4 \text{ км}\) — ширина участка.
в) Периметр участка:
\(2 \cdot (2,8 + 1,4) = 2 \cdot 4,2 = 8,4 \text{ км}\).
г) Площадь участка:
\(2,8 \cdot 1,4 = 3,92 \text{ км}^2\).
1) Пусть размеры первого участка на местности равны \(x\) см и \(y\) см. Для определения реальных размеров участка на местности, используя масштаб карты, необходимо составить пропорции между размером на карте и размером на местности. Масштаб указывает, что 1 см на карте соответствует 50 000 см на местности. Это означает, что если длина или ширина участка на карте известна, то реальный размер участка можно найти, умножив эту длину на 50 000.
а) Рассмотрим сначала длину участка. На карте длина равна 5,6 см. Составим пропорцию: \(5,6 : x = 1 : 50000\), где \(x\) — длина участка в сантиметрах на местности. Решая уравнение, получаем \(x = 5,6 \cdot 50000 = 280000\) см. Чтобы перевести сантиметры в более удобные единицы, делим на 100, получаем метры: \(280000 \div 100 = 2800\) м. Далее переводим метры в километры, деля на 1000: \(2800 \div 1000 = 2,8\) км. Таким образом, длина участка равна 2,8 км.
б) Аналогично определим ширину участка. На карте ширина равна 2,8 см. Составим пропорцию: \(2,8 : x = 1 : 50000\), где \(x\) — ширина участка в сантиметрах на местности. Решаем уравнение: \(x = 2,8 \cdot 50000 = 140000\) см. Переводим в метры: \(140000 \div 100 = 1400\) м, затем в километры: \(1400 \div 1000 = 1,4\) км. Значит, ширина участка равна 1,4 км.
в) Теперь найдем периметр участка, который равен сумме всех сторон. Поскольку участок прямоугольный, периметр вычисляется по формуле \(P = 2 \cdot (длина + ширина)\). Подставляем значения: \(2 \cdot (2,8 + 1,4) = 2 \cdot 4,2 = 8,4\) км. Это длина ограждения участка.
г) Для вычисления площади участка используем формулу площади прямоугольника \(S = длина \cdot ширина\). Подставляем значения: \(2,8 \cdot 1,4 = 3,92\) км\(^2\). Это реальная площадь участка на местности.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!