
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 2.89 Виленкин, Жохов — Подробные Ответы
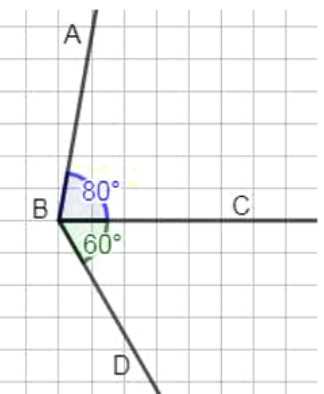
Проведите луч \(BC\) и постройте \(\angle ABC=80^\circ\) и \(\angle DBC=60^\circ\). Найдите угол \(ABD\). Проверьте ответ с помощью транспортира. Сколько решений имеет задача?
Пусть луч \(BC\) задан, и известны углы \(\angle ABC = 80^\circ\) и \(\angle DBC = 60^\circ\).
Первое решение:
Угол \( \angle ABD \) равен сумме углов \(\angle ABC\) и \(\angle DBC\), так как лучи \(BA\) и \(BD\) расположены по разные стороны от \(BC\).
То есть,
\(\angle ABD = \angle ABC + \angle DBC = 80^\circ + 60^\circ = 140^\circ\).
Второе решение:
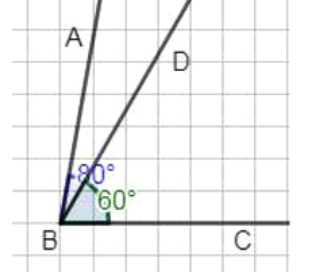
Если лучи \(BA\) и \(BD\) расположены по одну сторону от \(BC\), то угол \(\angle ABD\) равен разности углов \(\angle ABC\) и \(\angle DBC\):
\(\angle ABD = \angle ABC — \angle DBC = 80^\circ — 60^\circ = 20^\circ\).
Ответ:
Задача имеет два решения:
\(\angle ABD = 140^\circ\) и \(\angle ABD = 20^\circ\).
1. Рассмотрим луч \(BC\) и два угла, исходящих из точки \(B\): \(\angle ABC = 80^\circ\) и \(\angle DBC = 60^\circ\). Для построения угла \(\angle ABD\) необходимо понять взаимное расположение лучей \(BA\) и \(BD\) относительно луча \(BC\). Если лучи \(BA\) и \(BD\) расположены по разные стороны от луча \(BC\), тогда угол \(\angle ABD\) является внешним углом, который равен сумме углов \(\angle ABC\) и \(\angle DBC\). Это связано с тем, что при повороте от луча \(BA\) к лучу \(BD\) мы проходим через оба угла. Следовательно,
\(\angle ABD = \angle ABC + \angle DBC = 80^\circ + 60^\circ = 140^\circ\).
2. Второй случай возникает, если лучи \(BA\) и \(BD\) находятся по одну сторону от луча \(BC\). Тогда угол \(\angle ABD\) образуется как разность между углами \(\angle ABC\) и \(\angle DBC\). Это объясняется тем, что при движении от луча \(BA\) к лучу \(BD\) мы «вычитаем» угол \(\angle DBC\) из угла \(\angle ABC\), так как они расположены на одной стороне от \(BC\). В этом случае
\(\angle ABD = \angle ABC — \angle DBC = 80^\circ — 60^\circ = 20^\circ\).
Таким образом, при построении угла \(\angle ABD\) с заданными углами \(\angle ABC\) и \(\angle DBC\) возможны два варианта решения, зависящие от взаимного расположения лучей \(BA\) и \(BD\) относительно луча \(BC\). Первый вариант даёт угол \(140^\circ\), а второй — угол \(20^\circ\). Следовательно, задача имеет два решения:
\(\angle ABD = 140^\circ\) и \(\angle ABD = 20^\circ\).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!