ГДЗ по Математике 6 Класс Часть 1 Номер 2.80 Виленкин, Жохов — Подробные Ответы

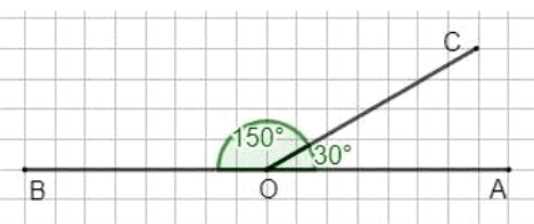
1) Развёрнутый угол \(AOB\) разделён на два угла: \(\angle AOC\) и \(\angle COB\). Чему равны эти углы, если угол \(\angle COB\) в 5 раз больше угла \(\angle AOC\)? Постройте эти углы.

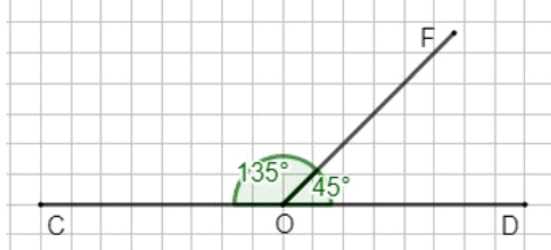
2) Развёрнутый угол \(COD\) разделён на два угла: \(\angle COF\) и \(\angle FOD\). Чему равны эти углы, если угол \(\angle FOD\) в 3 раза меньше угла \(\angle COF\)? Постройте эти углы.

1) Пусть \(\angle AOC = x\), тогда \(\angle COB = 5x\). Так как \(\angle AOB = 180^\circ\), составим уравнение:
\(x + 5x = 180\)
\(6x = 180\)
\(x = \frac{180}{6} = 30^\circ\) — \(\angle AOC\).
\(\angle COB = 5 \cdot 30 = 150^\circ\).

2) Пусть \(\angle FOD = x\), тогда \(\angle COF = 3x\). Так как \(\angle COD = 180^\circ\), составим уравнение:
\(x + 3x = 180\)
\(4x = 180\)
\(x = \frac{180}{4} = 45^\circ\) — \(\angle FOD\).
\(\angle COF = 3 \cdot 45 = 135^\circ\).

1) Рассмотрим развёрнутый угол \( \angle AOB \), который равен \( 180^\circ \). Этот угол разделён на два угла: \( \angle AOC \) и \( \angle COB \). Пусть величина угла \( \angle AOC \) равна \( x \) градусов. По условию, угол \( \angle COB \) в 5 раз больше угла \( \angle AOC \), то есть равен \( 5x \) градусов. Поскольку сумма этих двух углов должна быть равна развёрнутому углу, составим уравнение:
\( x + 5x = 180 \).
Это уравнение отражает факт, что сумма смежных углов равна \( 180^\circ \).

Далее упростим уравнение:
\( 6x = 180 \).
Чтобы найти \( x \), разделим обе части уравнения на 6:
\( x = \frac{180}{6} = 30^\circ \).
Таким образом, угол \( \angle AOC \) равен \( 30^\circ \).

Теперь найдём угол \( \angle COB \), умножив найденное значение \( x \) на 5:
\( \angle COB = 5 \cdot 30 = 150^\circ \).
Итог: \( \angle AOC = 30^\circ \), а \( \angle COB = 150^\circ \).

2) Рассмотрим развёрнутый угол \( \angle COD \), который также равен \( 180^\circ \). Этот угол разделён на два угла: \( \angle COF \) и \( \angle FOD \). По условию, угол \( \angle FOD \) в 3 раза меньше угла \( \angle COF \). Пусть величина угла \( \angle FOD \) равна \( x \) градусов, тогда угол \( \angle COF \) равен \( 3x \) градусов.

Сумма этих двух углов равна развёрнутому углу, поэтому составим уравнение:
\( x + 3x = 180 \).
Упростим уравнение:
\( 4x = 180 \).
Разделив обе части на 4, найдём \( x \):
\( x = \frac{180}{4} = 45^\circ \).
Это значение соответствует углу \( \angle FOD \).

Теперь найдём угол \( \angle COF \), умножив \( x \) на 3:
\( \angle COF = 3 \cdot 45 = 135^\circ \).
Итог: \( \angle FOD = 45^\circ \), а \( \angle COF = 135^\circ \).