
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 2.79 Виленкин, Жохов — Подробные Ответы
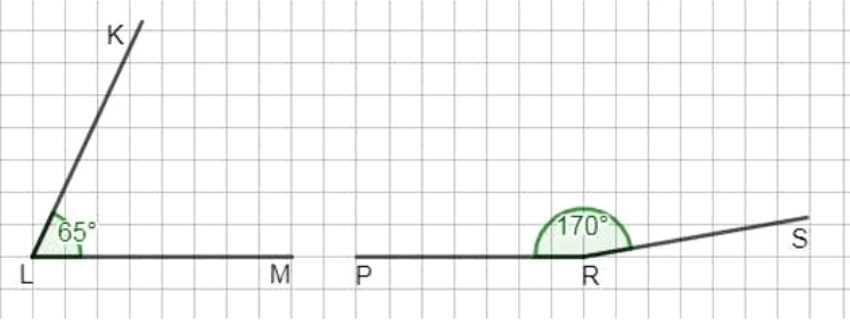
Используя транспортир, постройте \(\angle KLM=65^\circ\) и \(\angle PRS=170^\circ\).
Для построения угла \( \angle KLM = 65^\circ \) с вершиной в точке \( L \) нужно:
1. Провести луч \( LM \) горизонтально.
2. Отметить точку \( K \) так, чтобы угол между лучами \( LK \) и \( LM \) был равен \( 65^\circ \) с помощью транспортира.
Для построения угла \( \angle PRS = 170^\circ \) с вершиной в точке \( R \) нужно:
1. Провести луч \( PR \) горизонтально.
2. Отметить точку \( S \) так, чтобы угол между лучами \( RP \) и \( RS \) был равен \( 170^\circ \) с помощью транспортира.
Таким образом, углы построены согласно заданным величинам: \( \angle KLM = 65^\circ \) и \( \angle PRS = 170^\circ \).
Для построения угла \( \angle KLM = 65^\circ \) сначала необходимо провести луч \( LM \) горизонтально, который будет служить одной стороной угла. Затем с помощью транспортира размещаем его центр в точке \( L \), где находится вершина угла. Отметив на транспортере отметку \( 65^\circ \) от луча \( LM \), делаем метку на бумаге. После этого соединяем точку \( L \) с этой меткой, получая луч \( LK \). Таким образом, угол между лучами \( LK \) и \( LM \) равен \( 65^\circ \), что соответствует требуемому углу \( \angle KLM \).
Для построения угла \( \angle PRS = 170^\circ \) процесс похож, но угол значительно больше. Сначала проводим горизонтальный луч \( PR \). Затем центр транспортира ставим в точку \( R \), которая является вершиной угла. Чтобы построить угол \( 170^\circ \), на транспортере отмечаем отметку, соответствующую \( 170^\circ \) от луча \( RP \). Соединяем точку \( R \) с этой отметкой, получая луч \( RS \). Угол между лучами \( RP \) и \( RS \) теперь равен \( 170^\circ \), что и требовалось построить.
Таким образом, используя транспортир, мы можем точно измерить и построить углы заданной величины, ориентируясь на горизонтальную базовую сторону угла. Вершина угла всегда совпадает с центром транспортира, а стороны угла — это лучи, исходящие из вершины. Такой метод гарантирует точное построение углов \( \angle KLM = 65^\circ \) и \( \angle PRS = 170^\circ \).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!