ГДЗ по Математике 6 Класс Часть 1 Номер 2.489 Виленкин, Жохов — Подробные Ответы

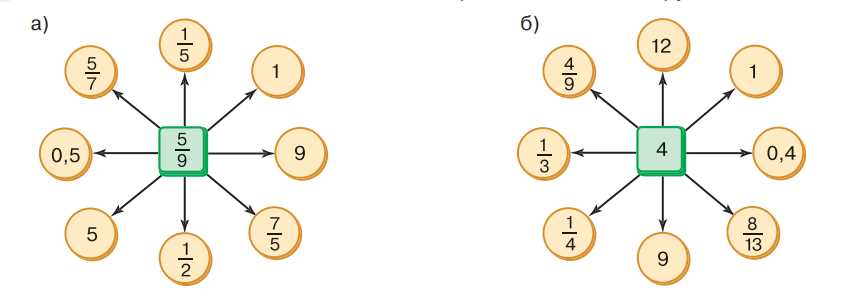
 Найдите частное от деления числа в квадратике на число в кружочках.

1) Решение дробных выражений:

\(\frac{5}{9} : \frac{1}{5} = \frac{5}{9} \cdot \frac{5}{1} = \frac{25}{9} = 2 \frac{7}{9}\);

\(\frac{5}{9} : 1 = \frac{5}{9}\);

\(\frac{5}{9} : 9 = \frac{5}{9} \cdot \frac{1}{9} = \frac{5}{81}\);

\(\frac{5}{9} : \frac{7}{5} = \frac{5}{9} \cdot \frac{5}{7} = \frac{25}{63}\);

\(\frac{5}{9} : \frac{1}{2} = \frac{5}{9} \cdot \frac{2}{1} = \frac{10}{9} = 1 \frac{1}{9}\);

\(\frac{5}{9} : 5 = \frac{5}{9} \cdot \frac{1}{5} = \frac{1}{9}\);

\(\frac{5}{9} : 0.5 = \frac{5}{9} \cdot \frac{1}{0.5} = \frac{5}{9} \cdot 2 = \frac{10}{9} = 1 \frac{1}{9}\);

\(\frac{5}{9} : \frac{5}{7} = \frac{5}{9} \cdot \frac{7}{5} = \frac{7}{9}\).

2) Решение с целыми и дробными числами:

\(4 : 12 = \frac{4}{12} = \frac{1}{3}\);

\(4 : 1 = 4\);

\(4 : 0.4 = 40 : 4 = 10\);

\(4 : \frac{8}{13} = 4 \cdot \frac{13}{8} = \frac{52}{8} = \frac{13}{2} = 6.5\);

\(4 : 9 = \frac{4}{9}\);

\(4 : \frac{1}{4} = 4 \cdot 4 = 16\);

\(4 : \frac{1}{3} = 4 \cdot 3 = 12\);

\(4 : \frac{4}{9} = 4 \cdot \frac{9}{4} = 9\).

1) Рассмотрим деление дроби \(\frac{5}{9}\) на разные числа и дроби. Деление дробей выполняется умножением на обратную дробь. Например, чтобы разделить \(\frac{5}{9}\) на \(\frac{1}{5}\), нужно умножить \(\frac{5}{9}\) на обратную к \(\frac{1}{5}\), то есть на \(\frac{5}{1}\). Получаем \( \frac{5}{9} \cdot \frac{5}{1} = \frac{25}{9} \). Эта дробь неправильная, поэтому выделяем целую часть: \( \frac{25}{9} = 2 \frac{7}{9} \). Таким образом, результат деления — смешанное число \(2 \frac{7}{9}\).

Если делить \(\frac{5}{9}\) на 1, то результат не изменится, так как любое число, делённое на 1, равно самому числу. Следовательно, \(\frac{5}{9} : 1 = \frac{5}{9}\).

Деление на целое число, например на 9, можно представить как умножение на дробь с числителем 1 и знаменателем 9: \( \frac{5}{9} : 9 = \frac{5}{9} \cdot \frac{1}{9} = \frac{5}{81} \). В этом случае дробь становится значительно меньше, так как знаменатель увеличился.

Деление \(\frac{5}{9}\) на дробь \(\frac{7}{5}\) также сводится к умножению на обратную дробь: \( \frac{5}{9} : \frac{7}{5} = \frac{5}{9} \cdot \frac{5}{7} = \frac{25}{63} \). Здесь мы перемножили числители и знаменатели соответственно. Результат — дробь, которую нельзя упростить дальше.

Аналогично, при делении \(\frac{5}{9}\) на \(\frac{1}{2}\) умножаем на обратную: \( \frac{5}{9} : \frac{1}{2} = \frac{5}{9} \cdot \frac{2}{1} = \frac{10}{9} \). Эта дробь неправильная, её можно представить как смешанное число \(1 \frac{1}{9}\).

Если делить \(\frac{5}{9}\) на 5, то это то же самое, что умножить на \(\frac{1}{5}\): \( \frac{5}{9} : 5 = \frac{5}{9} \cdot \frac{1}{5} = \frac{1}{9} \). Таким образом, дробь уменьшилась в 5 раз.

Для деления на 0,5 (половину) мы умножаем на обратное число, то есть на 2: \( \frac{5}{9} : 0.5 = \frac{5}{9} \cdot 2 = \frac{10}{9} = 1 \frac{1}{9} \). Получаем то же значение, что и при делении на \(\frac{1}{2}\).

Наконец, деление \(\frac{5}{9}\) на \(\frac{5}{7}\) сводится к умножению на обратную: \( \frac{5}{9} : \frac{5}{7} = \frac{5}{9} \cdot \frac{7}{5} = \frac{7}{9} \). Здесь происходит сокращение пятёрок, так как они есть и в числителе, и в знаменателе.

2) Теперь рассмотрим деление числа 4 на различные числа и дроби. Деление 4 на 12 — это то же самое, что дробь \(\frac{4}{12}\), которую можно сократить до \(\frac{1}{3}\). Это означает, что 4 разделить на 12 равно одной третьей.

Деление 4 на 1 даёт само число 4, так как любое число, делённое на 1, остаётся без изменений.

При делении 4 на 0,4 удобно умножить и делитель, и делимое на 10, чтобы избавиться от десятичных дробей: \(4 : 0.4 = 40 : 4 = 10\). Это упрощает вычисление.

Деление 4 на дробь \(\frac{8}{13}\) — это умножение 4 на обратную дробь \(\frac{13}{8}\): \(4 : \frac{8}{13} = 4 \cdot \frac{13}{8} = \frac{52}{8} = \frac{13}{2} = 6.5\). Здесь мы получили десятичное число.

Деление 4 на 9 — это дробь \(\frac{4}{9}\), которая уже в простом виде.

Если делить 4 на \(\frac{1}{4}\), то умножаем на 4: \(4 : \frac{1}{4} = 4 \cdot 4 = 16\). Это показывает, что деление на дробь меньше 1 увеличивает число.

Деление 4 на \(\frac{1}{3}\) — умножение на 3: \(4 : \frac{1}{3} = 4 \cdot 3 = 12\).

И наконец, деление 4 на \(\frac{4}{9}\) — умножение на обратную дробь \(\frac{9}{4}\): \(4 : \frac{4}{9} = 4 \cdot \frac{9}{4} = 9\). Здесь происходит сокращение числителя и знаменателя, что упрощает выражение.