
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 2.45 Виленкин, Жохов — Подробные Ответы
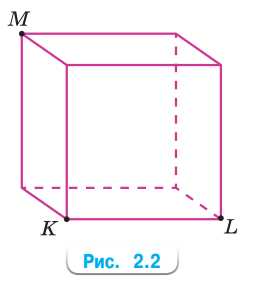
Развивай воображение. Найдите кратчайший путь на поверхности куба (рис. 2.2) из точки K в точку L:
а) который проходит через точку M;
б) который пересекает все горизонтальные рёбра куба, кроме ребра KL.
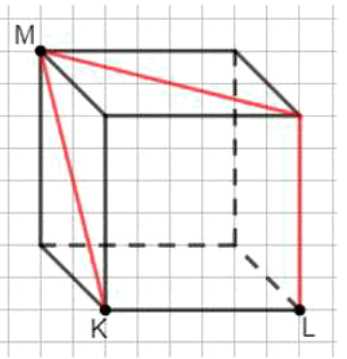
Кратчайший путь из точки \( K \) в точку \( L \), проходящий через точку \( M \), равен сумме отрезков \( KM + ML \). Так как \( KM = ML = a \) (ребро куба), длина пути равна \( 2a \).
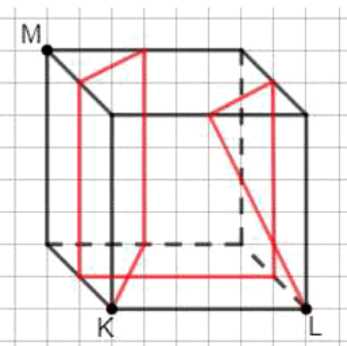
Кратчайший путь, пересекающий все горизонтальные рёбра куба, кроме ребра \( KL \), можно развернуть на плоскость. Такой путь будет равен длине прямой, соединяющей \( K \) и \( L \) по поверхности, обходя верхние рёбра. Длина пути равна \( 3a \).
1. Кратчайший путь из точки \( K \) в точку \( L \), проходящий через точку \( M \), состоит из двух отрезков: \( KM \) и \( ML \). Точки \( K \), \( L \), \( M \) расположены на рёбрах куба так, что каждый из этих отрезков равен длине ребра куба \( a \). Следовательно, длина пути равна сумме \( KM + ML = a + a = 2a \). Этот путь лежит на поверхности куба и является минимальным при условии прохождения через точку \( M \).
2. Для нахождения кратчайшего пути, который пересекает все горизонтальные рёбра куба, кроме ребра \( KL \), нужно рассмотреть развёртку поверхности куба. Горизонтальные рёбра — это рёбра, параллельные основанию куба. Исключая ребро \( KL \), путь должен пересечь остальные три горизонтальных ребра. Чтобы пройти через них, путь должен огибать куб по его боковым и верхним граням. На развёртке такой путь представляет собой прямую линию, соединяющую точки \( K \) и \( L \) через верхнюю грань и боковые рёбра.
Длина этого пути равна сумме трёх ребер куба, так как он проходит по трём рёбрам, пересекающим горизонтальные ребра, кроме \( KL \). Таким образом, длина равна \( 3a \). Этот путь является кратчайшим из всех, которые удовлетворяют условию пересечения указанных рёбер, и представляет собой ломаную линию по поверхности куба, обходящую нижнее ребро \( KL \).

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!