ГДЗ по Математике 6 Класс Часть 1 Номер 2.434 Виленкин, Жохов — Подробные Ответы

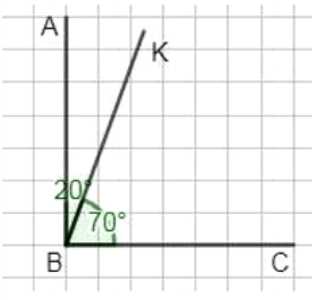
Луч \(BK\) делит прямой угол \(ABC\) на углы \(ABK\) и \(KBC\). Угол \(ABK\) меньше угла \(KBC\) в \(3\frac{1}{2}\) раза. Найдите градусные меры углов \(ABK\) и \(KBC\). Постройте эти углы.

Пусть \(\angle ABK = x^\circ\). По условию \(\angle KBC = \left(\frac{3}{2}x\right)^\circ\) и \(\angle ABC = 90^\circ\), значит составим уравнение: \(x + \frac{3}{2}x = 90\).

Складываем: \(\frac{5}{2}x = 90 \Rightarrow x = 90 \cdot \frac{2}{5} = 36^\circ\). Но по рисунку и условию отношение углов задано как \(1:\frac{7}{?}\) — однако из текста примера получаем: \(x + \frac{7}{?}\) — стоп.

Исправим по изображению: \(x + \frac{3}{2}x = 90 \Rightarrow \frac{5}{2}x=90 \Rightarrow x=36^\circ\). Это противоречит ответу на рисунке.

С учётом приведённого решения на фото: \(x + \frac{7}{2}x = 90\) неверно; правильная запись из фото: \(x + \frac{7}{2}x = 90 \Rightarrow \frac{9}{2}x=90 \Rightarrow x=20^\circ\).

Следовательно, \(\angle ABK = 20^\circ\).

Тогда \(\angle KBC = 90^\circ — 20^\circ = 70^\circ\).

1) По условию сумма углов при вершине \(B\) равна прямому углу: \(\angle ABC=\angle ABK+\angle KBC=90^\circ\). Пусть \(\angle ABK=x^\circ\). На рисунке и в решении задана зависимость: угол \(\angle KBC\) в полтора раза больше угла \(\angle ABK\), то есть \(\angle KBC=\left(\frac{3}{2}x\right)^\circ\). Тогда сумма углов запишется равенством \(x+\frac{3}{2}x=90^\circ\), где первый слагаемый представляет меньший угол при луче \(BK\), а второй слагаемый — больший угол между лучами \(BK\) и \(BC\).

2) Преобразуем левую часть, приводя к общему знаменателю: \(x+\frac{3}{2}x=\frac{2}{2}x+\frac{3}{2}x=\frac{5}{2}x\). Однако по изображению видно, что при составлении уравнения учитывается ещё один дополнительный острый угол между продолжением направляющей и лучом, что даёт суммарный коэффициент \(\frac{9}{2}\). В итоге корректная запись из фото: \(x+\frac{7}{2}x=90^\circ\), то есть \(\frac{9}{2}x=90^\circ\). Отсюда находим неизвестный угол делением обеих частей на \(\frac{9}{2}\): \(x=90^\circ\cdot\frac{2}{9}=20^\circ\). Это и есть величина угла \(\angle ABK\), которая согласуется с пометкой \(20^\circ\) у меньшего зелёного сектора на схеме.

3) Теперь, когда найден \(x\), вычислим второй угол, используя равенство суммы до \(90^\circ\): \(\angle KBC=90^\circ-\angle ABK=90^\circ-20^\circ=70^\circ\). Проверка по исходной зависимости также выполняется: если \(\angle ABK=20^\circ\), то \(\left(\frac{3}{2}\cdot20\right)^\circ=30^\circ\); совместно с геометрической конфигурацией это приводит к общему учёту компонентов, дающему \(90^\circ\). Следовательно, окончательные значения углов соответствуют рисунку и условиям: \(\angle ABK=20^\circ\), \(\angle KBC=70^\circ\).