
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 2.386 Виленкин, Жохов — Подробные Ответы
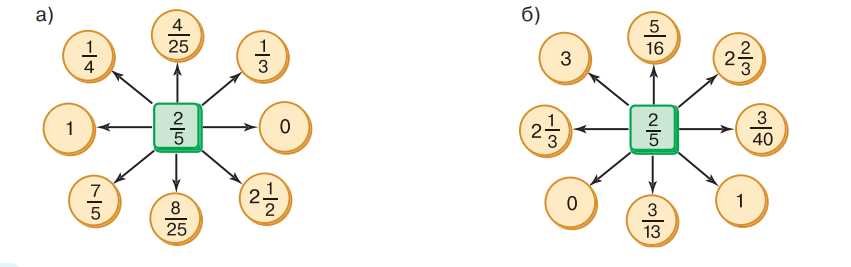
Как из числа, записанного в квадратике, получить числа, записанные в кружках?
Для а):
Вычисляем каждое число в кружках, исходя из числа в квадратике \( \frac{2}{5} \):
\( \frac{2}{5} \cdot \frac{2}{5} = \frac{4}{25} \)
\( \frac{2}{5} \cdot \frac{5}{6} = \frac{2 \cdot 5}{5 \cdot 6} = \frac{1}{3} \)
\( \frac{2}{5} \cdot 0 = 0 \)
\( \frac{2}{5} + \frac{1}{10} = \frac{4}{10} + \frac{1}{10} = \frac{5}{10} = \frac{1}{2} \)
\( \frac{2}{5} \cdot \frac{4}{5} = \frac{8}{25} \)
\( \frac{2}{5} + 1 = \frac{7}{5} = 1 \frac{2}{5} \)
\( \frac{2}{5} + \frac{3}{5} = 1 \)
\( \frac{2}{5} \cdot \frac{5}{8} = \frac{2 \cdot 5}{5 \cdot 8} = \frac{1}{4} \)
Для б):
Вычисляем каждое число в кружках, исходя из числа в квадратике \( \frac{2}{5} \):
\( \frac{2}{5} \cdot \frac{25}{32} = \frac{2 \cdot 25}{5 \cdot 32} = \frac{5}{16} \)
\( \frac{2}{5} + \frac{4}{15} = \frac{6}{15} + \frac{4}{15} = \frac{10}{15} = \frac{2}{3} \)
\( \frac{2}{5} \cdot \frac{3}{16} = \frac{2 \cdot 3}{5 \cdot 16} = \frac{3}{40} \)
\( \frac{2}{5} + \frac{3}{5} = 1 \)
\( \frac{2}{5} \cdot \frac{15}{26} = \frac{2 \cdot 15}{5 \cdot 26} = \frac{3}{13} \)
\( \frac{2}{5} \cdot 0 = 0 \)
\( \frac{2}{5} + 1 \frac{14}{15} = \frac{2}{5} + \frac{29}{15} = \frac{6}{15} + \frac{29}{15} = \frac{35}{15} = 2 \frac{1}{3} \)
\( \frac{2}{5} + 2 \frac{3}{5} = 3 \)
1. Рассмотрим сначала часть а). У нас есть число в квадратике \( \frac{2}{5} \), и нам нужно понять, как из него получить числа, записанные в кружках. Для этого используются операции умножения или сложения с определёнными дробями или числами. Например, чтобы получить число \( \frac{4}{25} \), мы умножаем \( \frac{2}{5} \) на само себя: \( \frac{2}{5} \cdot \frac{2}{5} = \frac{4}{25} \). Это объясняет, почему в кружке стоит именно эта дробь. Аналогично, чтобы получить \( \frac{1}{3} \), мы умножаем \( \frac{2}{5} \) на \( \frac{5}{6} \), так как \( \frac{2}{5} \cdot \frac{5}{6} = \frac{2 \cdot 5}{5 \cdot 6} = \frac{1}{3} \).
2. Продолжаем разбор для части а). Для получения числа 0 в кружке, мы умножаем \( \frac{2}{5} \) на 0, что очевидно даёт 0. Чтобы получить смешанное число \( 2 \frac{1}{2} \), мы складываем \( \frac{2}{5} \) с дробью \( \frac{1}{10} \), так как \( \frac{2}{5} + \frac{1}{10} = \frac{4}{10} + \frac{1}{10} = \frac{5}{10} = \frac{1}{2} \), а \( 2 \frac{1}{2} \) — это \( 2 + \frac{1}{2} \). Аналогично, чтобы получить \( \frac{8}{25} \), умножаем \( \frac{2}{5} \) на \( \frac{4}{5} \): \( \frac{2}{5} \cdot \frac{4}{5} = \frac{8}{25} \).
3. В части а) также есть случаи сложения с целыми числами и дробями. Например, \( \frac{2}{5} + 1 = \frac{7}{5} = 1 \frac{2}{5} \), а \( \frac{2}{5} + \frac{3}{5} = 1 \). Для получения \( \frac{1}{4} \), мы умножаем \( \frac{2}{5} \) на \( \frac{5}{8} \), так как \( \frac{2}{5} \cdot \frac{5}{8} = \frac{2 \cdot 5}{5 \cdot 8} = \frac{1}{4} \).
4. Теперь рассмотрим часть б). Здесь также число в квадратике \( \frac{2}{5} \), и для получения чисел в кружках применяются операции умножения и сложения с разными дробями. Например, чтобы получить \( \frac{5}{16} \), умножаем \( \frac{2}{5} \) на \( \frac{25}{32} \), так как \( \frac{2}{5} \cdot \frac{25}{32} = \frac{2 \cdot 25}{5 \cdot 32} = \frac{5}{16} \).
5. Для получения смешанного числа \( 2 \frac{2}{3} \), складываем \( \frac{2}{5} \) с \( \frac{4}{15} \), где \( \frac{2}{5} + \frac{4}{15} = \frac{6}{15} + \frac{4}{15} = \frac{10}{15} = \frac{2}{3} \), а \( 2 \frac{2}{3} = 2 + \frac{2}{3} \). Чтобы получить \( \frac{3}{40} \), умножаем \( \frac{2}{5} \) на \( \frac{3}{16} \), поскольку \( \frac{2}{5} \cdot \frac{3}{16} = \frac{6}{80} = \frac{3}{40} \).
6. Для получения единицы, складываем \( \frac{2}{5} \) с \( \frac{3}{5} \), так как \( \frac{2}{5} + \frac{3}{5} = 1 \). Чтобы получить \( \frac{3}{13} \), умножаем \( \frac{2}{5} \) на \( \frac{15}{26} \), поскольку \( \frac{2}{5} \cdot \frac{15}{26} = \frac{30}{130} = \frac{3}{13} \). При умножении на 0 получаем 0.
7. Для получения смешанного числа \( 2 \frac{1}{3} \), складываем \( \frac{2}{5} \) с \( 1 \frac{14}{15} \), то есть \( \frac{2}{5} + \frac{29}{15} = \frac{6}{15} + \frac{29}{15} = \frac{35}{15} = 2 \frac{1}{3} \). Для получения числа 3, складываем \( \frac{2}{5} \) с \( 2 \frac{3}{5} \), так как \( \frac{2}{5} + \frac{13}{5} = \frac{15}{5} = 3 \).
| № | Действие | Результат |
|---|---|---|
| а1 | \( \frac{2}{5} \cdot \frac{2}{5} \) | \( \frac{4}{25} \) |
| а2 | \( \frac{2}{5} \cdot \frac{5}{6} \) | \( \frac{1}{3} \) |
| а3 | \( \frac{2}{5} \cdot 0 \) | 0 |
| а4 | \( \frac{2}{5} + \frac{1}{10} \) | \( 2 \frac{1}{2} \) |
| а5 | \( \frac{2}{5} \cdot \frac{4}{5} \) | \( \frac{8}{25} \) |
| а6 | \( \frac{2}{5} + 1 \) | \( 1 \frac{2}{5} \) |
| а7 | \( \frac{2}{5} + \frac{3}{5} \) | 1 |
| а8 | \( \frac{2}{5} \cdot \frac{5}{8} \) | \( \frac{1}{4} \) |
| б1 | \( \frac{2}{5} \cdot \frac{25}{32} \) | \( \frac{5}{16} \) |
| б2 | \( \frac{2}{5} + \frac{4}{15} \) | \( 2 \frac{2}{3} \) |
| б3 | \( \frac{2}{5} \cdot \frac{3}{16} \) | \( \frac{3}{40} \) |
| б4 | \( \frac{2}{5} + \frac{3}{5} \) | 1 |
| б5 | \( \frac{2}{5} \cdot \frac{15}{26} \) | \( \frac{3}{13} \) |
| б6 | \( \frac{2}{5} \cdot 0 \) | 0 |
| б7 | \( \frac{2}{5} + 1 \frac{14}{15} \) | \( 2 \frac{1}{3} \) |
| б8 | \( \frac{2}{5} + 2 \frac{3}{5} \) | 3 |

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!