ГДЗ по Математике 6 Класс Часть 1 Номер 2.362 Виленкин, Жохов — Подробные Ответы

Практическая работа

Оборудование: карандаш, линейка, транспортир, плотная бумага, ножницы, клей.
а) Задание: склейте модель треугольной пирамиды (рис. 2.8, а).
Порядок работы:
1) На плотном листе бумаги постройте развёртку треугольной пирамиды по следующему алгоритму:
1. Постройте равносторонний треугольник, используя алгоритм зада- чи 1.136, с. 34. Сторону треугольника возьмите больше 12 см, но меньше 20 см.
2. Разделите каждую сторону треугольника пополам и соедините точки де- ления отрезками.
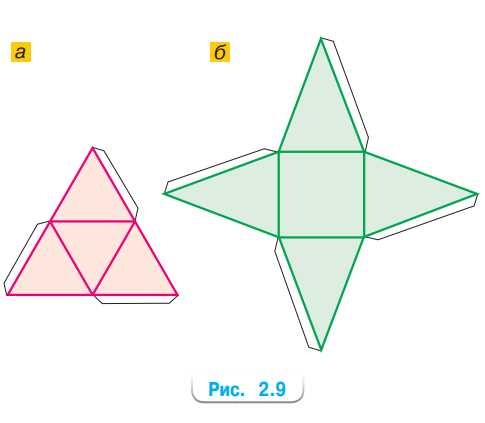
2) Нарисуйте клапаны (рис. 2.9, а).
3) Склейте модель треугольной пирамиды.
б) Задание: сделайте модель четырёхугольной пирамиды (рис. 2.8, б).
Порядок работы:
1) На плотном листе бумаги постройте развёртку четырёхугольной пирамиды по следующему алгоритму:
1. Постройте квадрат, сторона которого больше 6 см, но меньше 10 см.
2. На сторонах квадрата постройте одинаковые равнобедренные треугольни- ки, используя алгоритм задачи 1.136, с. 34 (сторона квадрата — основание равнобедренного треугольника). Боковую сторону треугольника возьмите больше 8 см, но меньше 16 см.
2) Нарисуйте клапаны (рис. 2.9, б).
3) Склейте модель четырёхугольной пирамиды.

а) Треугольная пирамида (регулярный тетраэдр).
— Постройте равносторонний треугольник со стороной \(12< a <20\) см. - Отметьте середины сторон, соедините их отрезками — получится три равносторонних треугольника внутри. Это и есть развёртка: центральный треугольник и три боковых, соединённых по его сторонам. - По внешним рёбрам добавьте клапаны шириной \(0{,}5\!-\!1\) см, надрежьте, согните по рёбрам и склейте грани попарно. б) Четырёхугольная пирамида. - Постройте квадрат со стороной \(6< b <10\) см. - На каждой стороне постройте равнобедренный треугольник с основанием \(b\) и боковой стороной \(8< c <16\) см; вершины направлены наружу — получится «крест» из четырёх одинаковых треугольников вокруг квадрата. - По внешним рёбрам треугольников и части рёбер квадрата нарисуйте клапаны шириной \(0{,}5\!-\!1\) см, вырежьте, согните по линиям и склейте боковые грани, совместив рёбра основания квадрата.

а) Треугольная пирамида.
1) Построение развертки. На плотной бумаге с помощью линейки отметьте отрезок желаемой длины стороны равностороннего треугольника \(a\) так, чтобы выполнялось \(12<a<20\) см. Постройте равносторонний треугольник по алгоритму задачи 1.136: от каждой конечной точки отрезка опишите дуги окружностей радиусом \(a\), найдите их пересечение и соедините вершины с концами основания. Далее найдите середины всех трех сторон: отложите на каждой стороне точки, удаленные от концов на \(\frac{a}{2}\). Соедините эти средние точки отрезками, получив три внутренних отрезка, которые делят исходный треугольник на 4 равных по площади маленьких равносторонних треугольника со стороной \(\frac{a}{2}\). Для развертки выберите один из центральных малых треугольников как базовый и вокруг него расположите три таких же треугольника, присоединенные по его сторонам; ориентируйте их так, чтобы они образовали «веер» из трех граней, как на рисунке. Линии соединения служат линиями сгиба, их удобно наметить тупой стороной ножниц или пустым стержнем, не прорезая бумагу.

2) Клапаны. По всем внешним контурам получившихся трех боковых треугольников и по двум-трем сторонам базового треугольника добавьте клеевые клапаны одинаковой ширины \(0{,}5\!-\!1\) см. Клапаны рисуют как узкие полосы под небольшим углом, чтобы при сгибе не возникало нахлестов; на вершинах делайте небольшие косые срезы. Линии сгиба отметьте штрихпунктиром, а линии реза — сплошной линией. Вырежьте заготовку аккуратно по внешнему контуру, не разрезая по линиям сгиба. Перед склейкой предварительно согните все рёбра внутрь по намеченным линиям.

3) Склейка. Нанесите тонкий равномерный слой клея на клапаны, последовательно соединяя соседние грани: сначала приклейте две боковые грани к базовой, затем замкните третьей. Совмещайте рёбра попарно, контролируя совпадение длин рёбер \(a\) и отсутствие щелей. После фиксации граней соедините оставшийся клапан, замкнув фигуру в пространстве. При необходимости используйте прищепки до высыхания. Готовая модель — равносторонняя треугольная пирамида с одинаковыми рёбрами длины \(a\), высота такой пирамиды при равностороннем основании равна \(h=\frac{\sqrt{6}}{3}\,a\) и служит проверкой пропорций при визуальном осмотре.

б) Четырёхугольная пирамида.
1) Построение развертки. На плотной бумаге постройте квадрат со стороной \(b\), где \(6<b<10\) см. Проверьте равенство всех сторон и прямые углы. На каждой стороне квадрата постройте равнобедренный треугольник с основанием, совпадающим со стороной квадрата, и одинаковыми боковыми сторонами длины \(c\), где \(8<c<16\) см. Для этого на продолжении перпендикуляра к середине каждой стороны отложите точку, находящуюся на расстоянии \(h_{\triangle}\) от основания, где \(h_{\triangle}=\sqrt{c^{2}-\left(\frac{b}{2}\right)^{2}}\). Соедините эту вершину с концами соответствующей стороны квадрата — получится одинаковый «крест» из четырех треугольников вокруг квадрата-основания. Линии присоединения треугольников к квадрату — линии сгиба боковых граней.

2) Клапаны. По внешним боковым рёбрам всех четырех треугольников добавьте клеевые клапаны шириной \(0{,}5\!-\!1\) см; уместно сделать клапаны на одной боковой стороне каждого треугольника и на двух смежных сторонах квадрата, чтобы было удобно замыкать модель. На вершинах клапаны подрежьте под углом, чтобы при склейке не выступали. Обозначьте штрихпунктиром линии сгиба по рёбрам квадрата и по боковым рёбрам треугольников, сплошной линией — линии реза. Вырежьте развертку целиком, не отделяя треугольники от квадрата. Аккуратно намечайте сгиб по линейке, проводя тупым предметом по линиям сгиба.

3) Склейка. Предварительно согните все боковые треугольники вверх относительно квадрата. Нанесите клей на соответствующие клапаны и последовательно соединяйте соседние боковые грани попарно, совмещая рёбра длины \(c\). После фиксации трех граней замкните четвертую, используя оставшийся клапан; прижмите соединения до схватывания. Контролируйте, чтобы основание оставалось плоским и квадратным со стороной \(b\), а вершины треугольников сходились без зазоров; высота пирамиды при выбранных \(b\) и \(c\) должна удовлетворять \(h=\sqrt{c^{2}-\left(\frac{b}{2}\right)^{2}}\). Для проверки параллельности основания поверхности стола измерьте диагонали квадрата: они равны \(d=b\sqrt{2}\); совпадение диагоналей и симметрия граней подтверждают корректность склейки.