
ГДЗ к учебнику Виленкина для 6 класса, часть 1 (авторы Жохов, Чесноков, Виленкин) — это удобный ориентир по базовым темам начала курса, где формируется фундамент математической грамотности: от понимания натуральных чисел и порядка действий до уверенной работы с обыкновенными дробями, признаками делимости, НОД и НОК, первыми задачами на проценты и элементарными уравнениями. Правильно составленный решебник отражает структуру учебника и помогает выстроить у ученика устойчивую привычку следить за логикой решения, сопоставлять шаги с теорией.
ГДЗ по Математике 6 Класс Часть 1 Номер 2.31 Виленкин, Жохов — Подробные Ответы
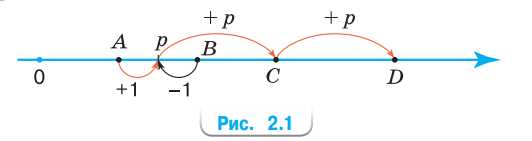
Существуют ли среди точек A, B, C и D точки, координаты которых простые числа (рис. 2.1), если \(p\) — простое число?
Если \(p\) — простое число, то:
Координаты точек:
\(A = p — 1\),
\(B = p\),
\(C = p + 1\),
\(D = p + p = 2p\).
Если \(p = 3\), то \(A = 2\) — простое число.
Если \(p = 2\), то \(B = 3\) — простое число и \(C = 5\) — простое число.
Таким образом, среди точек \(A, B, C, D\) при простом \(p\) могут быть точки с координатами, являющимися простыми числами.
Если \(p\) — простое число, то координаты точек на числовой оси определяются следующим образом: точка \(A\) имеет координату \(p — 1\), точка \(B\) — координату \(p\), точка \(C\) — координату \(p + 1\), а точка \(D\) — координату \(2p\). Здесь \(p\) — переменная, принимающая значения простых чисел. Рассмотрим, какие из этих координат могут быть простыми числами.
Во-первых, если взять \(p = 3\), то координаты будут \(A = 3 — 1 = 2\), \(B = 3\), \(C = 4\), \(D = 6\). Среди них число \(2\) — простое, \(3\) — простое, \(4\) и \(6\) — составные числа. Значит, при \(p = 3\) точка \(A\) имеет координату, являющуюся простым числом. Во-вторых, если \(p = 2\), то координаты будут \(A = 1\), \(B = 2\), \(C = 3\), \(D = 4\). Здесь \(B = 2\) и \(C = 3\) — простые числа, \(A = 1\) не считается простым, \(D = 4\) — составное. Таким образом, при \(p = 2\) точки \(B\) и \(C\) имеют простые координаты.
Из этого следует, что при любом простом \(p\) некоторые из точек \(A, B, C, D\) могут иметь координаты, являющиеся простыми числами. При этом точка \(B\) всегда находится в позиции \(p\), которая по определению простая, так как \(p\) — простое число. Точки \(A\) и \(C\), расположенные на единицу левее и правее \(p\), могут быть простыми в зависимости от конкретного значения \(p\). Точка \(D\) с координатой \(2p\) всегда будет составным числом, так как она кратна \(p\) и больше \(p\). Таким образом, среди данных точек обязательно существуют точки с простыми координатами, если \(p\) — простое число.

Любой навык лучше отрабатывать самостоятельной практикой, и решение задач — не исключение. Прежде чем обратиться к подсказкам, стоит попробовать справиться с заданием, опираясь на свои знания. Если дойти до конца удалось — проверить ответ и в случае расхождений сверить своё решение с правильным.





Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!