ГДЗ по Математике 6 Класс Часть 1 Номер 2.289 Виленкин, Жохов — Подробные Ответы

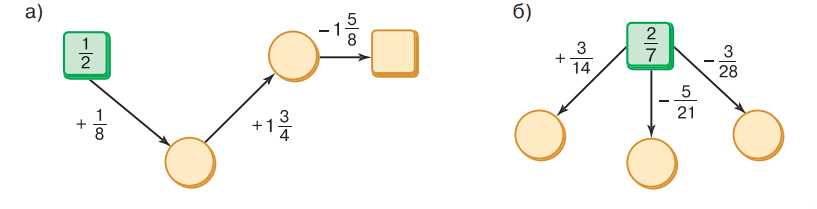
Найдите числа, которых не хватает в цепочке и на схеме.

Для а):

Сначала складываем \( \frac{1}{2} + \frac{1}{8} = \frac{4}{8} + \frac{1}{8} = \frac{5}{8} \).

Затем \( \frac{5}{8} + 1 \frac{3}{4} = \frac{5}{8} + \frac{7}{4} = \frac{5}{8} + \frac{14}{8} = \frac{19}{8} = 2 \frac{3}{8} \).

Далее \( 2 \frac{3}{8} — 1 \frac{5}{8} = \frac{19}{8} — \frac{13}{8} = \frac{6}{8} = \frac{3}{4} \).

Ответы: \( \frac{5}{8} \), \( 2 \frac{3}{8} \), \( \frac{3}{4} \).

Для б):

Складываем \( \frac{2}{7} + \frac{3}{14} = \frac{4}{14} + \frac{3}{14} = \frac{7}{14} = \frac{1}{2} \).

Вычитаем \( \frac{2}{7} — \frac{5}{21} = \frac{6}{21} — \frac{5}{21} = \frac{1}{21} \).

Вычитаем \( \frac{2}{7} — \frac{3}{28} = \frac{8}{28} — \frac{3}{28} = \frac{5}{28} \).

Ответы: \( \frac{1}{2} \), \( \frac{1}{21} \), \( \frac{5}{28} \).

1) Рассмотрим часть а). Начинаем с первого сложения: нужно сложить числа \( \frac{1}{2} \) и \( \frac{1}{8} \). Чтобы сложить дроби, нужно привести их к общему знаменателю. Знаменатели 2 и 8, общий знаменатель будет 8. Переводим \( \frac{1}{2} \) в дробь с знаменателем 8, получаем \( \frac{4}{8} \). Теперь складываем \( \frac{4}{8} + \frac{1}{8} = \frac{5}{8} \). Это число и есть первое пропущенное значение в цепочке.

2) Следующий шаг — прибавить к \( \frac{5}{8} \) число \( 1 \frac{3}{4} \). Для удобства переведём смешанное число в неправильную дробь: \( 1 \frac{3}{4} = \frac{7}{4} \). Чтобы сложить \( \frac{5}{8} + \frac{7}{4} \), нужно привести дроби к общему знаменателю. Знаменатели 8 и 4, общий знаменатель 8. Переводим \( \frac{7}{4} \) в дробь с знаменателем 8: \( \frac{14}{8} \). Складываем: \( \frac{5}{8} + \frac{14}{8} = \frac{19}{8} \). Это неправильная дробь, её можно представить как смешанное число: \( 2 \frac{3}{8} \). Это второе пропущенное число.

3) Теперь нужно вычесть из \( 2 \frac{3}{8} \) число \( 1 \frac{5}{8} \). Переведём оба числа в неправильные дроби: \( 2 \frac{3}{8} = \frac{19}{8} \), \( 1 \frac{5}{8} = \frac{13}{8} \). Вычитаем: \( \frac{19}{8} — \frac{13}{8} = \frac{6}{8} \). Упростим дробь: \( \frac{6}{8} = \frac{3}{4} \). Это третье пропущенное число в цепочке.

4) Рассмотрим часть б). Сначала нужно сложить числа \( \frac{2}{7} \) и \( \frac{3}{14} \). Чтобы сложить эти дроби, приведём их к общему знаменателю. Знаменатели 7 и 14, общий знаменатель 14. Переводим \( \frac{2}{7} \) в дробь с знаменателем 14: \( \frac{4}{14} \). Складываем: \( \frac{4}{14} + \frac{3}{14} = \frac{7}{14} \). Упрощаем дробь: \( \frac{7}{14} = \frac{1}{2} \). Это первое пропущенное число в части б).

5) Далее вычитаем из \( \frac{2}{7} \) число \( \frac{5}{21} \). Общий знаменатель для 7 и 21 — 21. Переводим \( \frac{2}{7} \) в дробь с знаменателем 21: \( \frac{6}{21} \). Вычитаем: \( \frac{6}{21} — \frac{5}{21} = \frac{1}{21} \). Это второе пропущенное число.

6) Последнее действие — вычесть из \( \frac{2}{7} \) число \( \frac{3}{28} \). Общий знаменатель для 7 и 28 — 28. Переводим \( \frac{2}{7} \) в дробь с знаменателем 28: \( \frac{8}{28} \). Вычитаем: \( \frac{8}{28} — \frac{3}{28} = \frac{5}{28} \). Это третье пропущенное число в части б).

Ответы:
а) \( \frac{5}{8} \), \( 2 \frac{3}{8} \), \( \frac{3}{4} \)
б) \( \frac{1}{2} \), \( \frac{1}{21} \), \( \frac{5}{28} \)