ГДЗ по Математике 6 Класс Часть 1 Номер 2.235 Виленкин, Жохов — Подробные Ответы

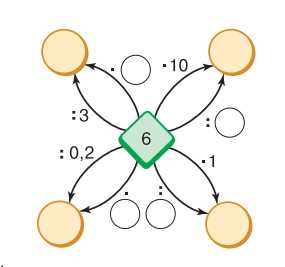
Найдите числа, которых не хватает на схеме справа.

\(6 \cdot 10 = 60\) — умножение числа 6 на 10 даёт 60.

\(6 \cdot 1 = 6\) — умножение на 1 не меняет число.

\(6 : 0,2 = 30\) — деление 6 на 0,2 эквивалентно умножению на 5, получается 30.

\(6 : 3 = 2\) — деление 6 на 3 даёт 2.

\(6 : 60 = 0,1\) — деление 6 на 60 даёт десятичную дробь 0,1.

\(6 : 6 = 1\) — число, делённое само на себя, равно 1.

\(30 : 6 = 5\) — деление 30 на 6 даёт 5.

\(2 : 6 = \frac{2}{6} = \frac{1}{3}\) — деление 2 на 6 выражается в виде дроби, которая сокращается до \(\frac{1}{3}\).

1. Рассмотрим выражение \(6 \cdot 10 = 60\). Здесь мы умножаем число 6 на 10. Умножение на 10 означает, что мы увеличиваем число в 10 раз, то есть просто добавляем один ноль к числу 6. Это базовое свойство умножения, которое позволяет быстро вычислять произведения с десятками. Таким образом, результат равен 60, что подтверждается простым подсчётом.

2. В выражении \(6 \cdot 1 = 6\) умножение на 1 не изменяет значение числа. Это свойство единицы в арифметике: любое число, умноженное на 1, остаётся самим собой. Это важное правило, которое часто используется для упрощения вычислений и проверки правильности действий.

3. Деление \(6 : 0,2 = 30\) можно понять через преобразование деления на десятичную дробь. Деление на 0,2 эквивалентно умножению на обратное число, то есть на 5, поскольку \(0,2 = \frac{2}{10} = \frac{1}{5}\). Следовательно, \(6 : 0,2 = 6 \cdot 5 = 30\). Это показывает связь между делением на дроби и умножением на их обратные значения.

4. В выражении \(6 : 3 = 2\) делим число 6 на 3. Деление означает разбиение числа на равные части. Здесь 6 разбивается на 3 части, каждая из которых равна 2. Это простое деление, демонстрирующее, как можно распределить количество поровну.

5. Деление \(6 : 60 = 0,1\) показывает, что при делении меньшего числа на большее получается десятичная дробь, меньшая единицы. В данном случае 6 разделено на 60, что даёт \(0,1\), то есть одну десятую. Это иллюстрирует, как деление может приводить к дробным результатам.

6. Выражение \(6 : 6 = 1\) отражает фундаментальное свойство чисел: любое число, делённое на само себя, равно 1. Это связано с тем, что число содержится в себе ровно один раз, поэтому результат деления всегда единица.

7. При делении \(30 : 6 = 5\) мы делим 30 на 6. Это означает, что 30 разбивается на 6 равных частей, и каждая часть равна 5. Таким образом, 6 умещается в 30 ровно 5 раз.

8. В выражении \(2 : 6 = \frac{2}{6} = \frac{1}{3}\) деление двух чисел даёт дробь. Здесь 2 делится на 6, что можно записать как дробь \(\frac{2}{6}\). Эту дробь можно упростить, сократив числитель и знаменатель на 2, получая \(\frac{1}{3}\). Это показывает, как деление приводит к дробным значениям и как их можно упрощать.

9. Все эти операции демонстрируют основные свойства умножения и деления, а также связь между ними. Умножение на целые числа и деление на десятичные дроби тесно связаны через понятие обратных чисел.

10. Понимание этих примеров важно для дальнейшего изучения математики, так как они показывают, как работать с разными типами чисел и как переходить от целых чисел к дробям и десятичным дробям, используя базовые арифметические операции.